PB
4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
8 tháng 5 2016
Tháng 3 năm 2014 có 31 ngày, tháng 4 năm 2014 có 30 ngày.
Thứ bày là ngày 29/3 nên số ngày còn lại của tháng 3 là:
31 – 29 = 2 (ngày)
Tổng số ngày còn lại của tháng 3 và số ngày tháng 4 là:
2 + 30 = 32 (ngày)
Ta thấy: 32 : 7 = 4 (tuần) dư 4 ngày
Các ngày đó là: Chủ nhật, Thứ hai, Thứ ba và Thứ tư.
Thứ Tư ứng với ngày 30/4/2014 nên ngày Chủ nhật cuối cùng trong tháng 4/2014 là ngày27/4/2014
8 tháng 5 2016
Tháng 3 năm 2014 có 31 ngày, tháng 4 năm 2014 có 30 ngày.
Thứ bảy là ngày 29/3 nên số ngày còn lại của tháng 3 là:
31 – 29 = 2 (ngày)
Tổng số ngày còn lại của tháng 3 và số ngày tháng 4 là:
2 + 30 = 32 (ngày)
Ta thấy: 32 : 7 = 4 (tuần) dư 4
Các ngày đó là: Chủ Nhật, Thứ 2, Thứ 3 và Thứ 4.
Thứ 4 ứng với ngày 30/4/2014 nên ngày Chủ nhật cuối cùng trong tháng 4/2014 là ngày 27/4/2014
HQ
Hà Quang Minh
Giáo viên
28 tháng 9 2023
a) Nhiệt độ trung bình trong năm ở Hà Nội là: \(\overline X = \frac{{16,4 + 17,0 + 20,2 + 23,7 + 27,3 + 28,8 + 28,9 + 28,2 + 27,2 + 24,6 + 21,4 + 18,2}}{{12}} = 23,5\)
b) Nhiệt độ trung bình của tháng có giá trị thấp nhất là: \(16,4\left( {^oC} \right)\)
Nhiệt độ trung bình của tháng có giá trị cao nhất là: \(28,9\left( {^oC} \right)\)
HQ
Hà Quang Minh
Giáo viên
30 tháng 9 2023
a) Tổng số tiền mẹ Việt rút ra được là:
\(T = 2\;000\;000\;000.{(1 + 7\% )^3} = 2\;450\;086\;000\)(đồng)
b) Với số tiền nêu trên, mẹ Việt mua được căn hộ chung cư với diện tích là:
\(2\;450\;086\;000:30\;626\;075 = 80\)(mét vuông)
TRAO ĐỔI
Để mua được căn hộ 100 mét vuông, cần số tiền là:
\(30\;626\;075.100 = 3\;062\;607\;500\)(đồng)
Gọi A là số tiền gửi vào (đơn vị đồng).
Ở thời điểm tháng 1 năm 2021, số tiền thu được là:
\(\begin{array}{l}T = A.{(1 + 7\% )^3} = 3\;062\;607\;500\\ \Rightarrow A = 3\;062\;607\;500:{(1 + 7\% )^3} = 2\;500\;000\;000\end{array}\)
Vậy để mua được căn hộ 100 mét vuông ở thời điểm tháng 1 năm 2021, mẹ Việt cần phải gửi tiết kiệm từ tháng 1 năm 2018 số tiền là 2 500 000 000 đồng.
TT
3
7 tháng 5 2016
Gọi số ngày của tháng đó là a. Theo công thức tính số số hạng trong dãy số cách đều thì
Số số hạng = (Số cuối - số đầu) : khoảng cách + 1
Ta có: 5 = (a - 1) : 7 + 1
a = 29
Vậy tháng Hai có 5 ngày Chủ nhật thì tháng Hai đó có 29 ngày.
+ Cách 2: Vẽ sơ đồ (chú ý tháng Hai chỉ có 28 hoặc 29 ngày)
5 ngày Chủ nhật sẽ là: ngày 1, 8, 17, 22, 29.
Vậy tháng Hai có 5 ngày Chủ nhật thì tháng Hai đó có 29 ngày.
HQ
Hà Quang Minh
Giáo viên
23 tháng 9 2023
a) Phát biểu “Tích hai số thực trái dấu là một số thực âm” là một mệnh đề toán học.
b) Phát biểu “Mọi số tự nhiên đều là dương” là một mệnh đề toán học.
c) Phát biểu “Có sự sống ngoài Trái Đất” không là một mệnh đề toán học (vì không liên quan đến sự kiện Toán học nào).
d) Phát biểu “Ngày 1 tháng 5 là ngày Quốc tế Lao động” không là một mệnh đề toán học (vì không liên quan đến sự kiện Toán học nào).
HQ
Hà Quang Minh
Giáo viên
28 tháng 9 2023
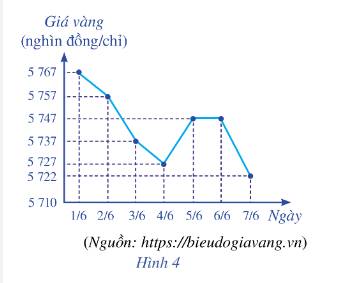
a) Dựa vào biểu đồ, ta có mẫu số liệu là:
5767 5757 5737 5727 5747 5747 5722
b) Khoảng biến thiên của mẫu số liệu đó là: \(R = {x_{\max }} - {x_{\min }} = 5767 - 5722 = 45\)
c) +) Sắp xếp mẫu số liệu theo thứ tự không giảm, ta có:
5722 5727 5737 5747 5747 5757 5767
+) Các tứ phân vị của mẫu số liệu là:
Trung vị của mẫu số liệu: \({Q_2}\) = 5747.
Trung vị của dãy 5722 5727 5737 là: \({Q_1}\) = 5727.
Trung vị của dãy 5747 5757 5767 là: \({Q_3}\) = 5757.
+) Khoảng tứ phân vị của mẫu số liệu là: \({\Delta _Q} ={Q_3} - {Q_1}\) = 5757- 5727= 30.
d) +) Giá vàng trung bình trong 7 ngày đầu tiên của tháng 6 năm 2021 là: \(\overline x = \frac{{5722{\rm{ + }}5727{\rm{ + }}5737{\rm{ + }}5747{\rm{ + }}5747{\rm{ + }}5757{\rm{ + }}5767}}{7} = 5743,43\) ( nghìn đồng/ chỉ)
+) Phương sai của mẫu số liệu là: \({s^2} = \frac{{\left[ {{{\left( {5722 - \overline x } \right)}^2} + {{\left( {5727 - \overline x } \right)}^2} + ... + {{\left( {5767 - \overline x } \right)}^2}} \right]}}{7} \approx 219,39\)
+) Độ lệch chuẩn của của mẫu số liệu là: \(s = \sqrt {{s^2}} = \sqrt {219,39} \approx 14,81\)( nghìn đồng/ chỉ)
HQ
Hà Quang Minh
Giáo viên
26 tháng 9 2023
a) Năm 2019:
+) Số trung bình: \(\overline x = \frac{{54 + 22 + 24 + 30 + 35 + 40 + 31 + 29 + 29 + 37 + 40 + 31}}{{12}} = 33,5\)
+) Phương sai \({S^2} = \frac{1}{{12}}\left( {{{54}^2} + {{22}^2} + ... + {{31}^2}} \right) - 33,{5^2} = 67,25\) => Độ lệch chuẩn \(S = \sqrt {{S^2}} \approx 8,2\)
+) Khoảng tứ phân vị: \({\Delta _Q} = {Q_3} - {Q_1}\)
Sắp xếp mẫu số liệu theo thứ tự không giảm: 22, 24, 29, 29, 30, 31, 31, 35, 37, 40, 40, 54
\({Q_2} = {M_e} = \frac{1}{2}(31 + 31) = 31\)
\({Q_1}\) là trung vị của nửa số liệu: 22, 24, 29, 29, 30, 31. Do đó \({Q_1} = 29\)
\({Q_3}\) là trung vị của nửa số liệu: 31, 35, 37, 40, 40, 54. Do đó \({Q_3} = 38,5\)
\( \Rightarrow {\Delta _Q} = 38,5 - 29 = 9,5\)
Năm 2020:
+) Số trung bình: \(\overline x = 34,5\)
+) Phương sai \({S^2} = \frac{1}{{12}}\left( {{{45}^2} + {{28}^2} + ... + {{37}^2}} \right) - 34,{5^2} = 15,75\) => Độ lệch chuẩn \(S = \sqrt {{S^2}} \approx 3,97\)
+) Khoảng tứ phân vị: \({\Delta _Q} = {Q_3} - {Q_1}\)
Sắp xếp mẫu số liệu theo thứ tự không giảm: 28, 31, 32, 33, 33, 34, 34, 35, 35, 37, 37, 45.
\({Q_2} = {M_e} = \frac{1}{2}(34 + 34) = 34\)
\({Q_1}\) là trung vị của nửa số liệu: 28, 31, 32, 33, 33, 34. Do đó \({Q_1} = 32,5\)
\({Q_3}\) là trung vị của nửa số liệu: 34, 35, 35, 37, 37, 45. Do đó \({Q_3} = 36\)
\( \Rightarrow {\Delta _Q} = 36 - 32,5 = 3,5\)
b) Nhận xét:
So sánh số trung bình: số lượng bán ra trung bình theo tháng không tăng nhiều so với năm trước (tăng 1)
So sánh độ lệch chuẩn: Số lượng xe bán ra năm 2020 không có sự chênh lệch quá nhiều giữa các tháng.
=> Tác động của chiến lược: Số lượng xe bán ra tăng ít, nhưng đồng đều giữa các tháng.
ta có : 2020 \(⋮\)4 nên năm 2020 là năm nhuận và có 366 ngày
Mà 25 là thứ 2 nên cứ sau 1 tuần ( 7 ngày ) thì lại có 1 ngày thứ 2
có : 366 : 7=52 dư 2
vậy sau 366 ngày là \(\approx\) 52 tuần và 2 ngày là thứ 2+2=4
Vậy ngày 25 tháng 5 năm 2021 là thứ 4
Vì năm 2021 là năm không nhuận nên có 365 ngày.
Ta co: 365 : 7 = 52( dư 1)
Ta thêm 1 ngày vào thứ 2 thì ra thứ 3.