Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi số trứng của người thứ nhất là X.
Số trứng của người thứ hai là 100-X
Theo giải thiết ta có :
Trứng của người thứ nhất có giá là : 90000/100-X
Trứng của người thứ hai có giá là : 40000/X
Ta có hệ phương trình:
(90000/100-X)X=(40000/X)(100-X)
Giải hệ phương trình ta có:
X1=40
X2=-200 (loại)

Gọi x (quả) là số trứng của người thứ nhất.
Điều kiện: x ∈N*, x < 100
Khi đó số trứng của người thứ hai là 100 – x (quả)
Giá tiền một quả trứng của người thứ nhất là 15/(100 - x) (đồng)
Giá tiền một quả trứng của người thứ hai là 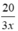 (đồng)
(đồng)
Số tiền người thứ nhất bán được là:
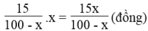
Số tiền người thứ hai bán được là:
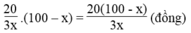
Theo đề bài, ta có phương trình:
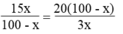
⇔ 45 x 2 = 20 100 - x 2 ⇔ 45 x 2 = 20(10000 – 200x + x 2 )
⇔ 45 x 2 = 200000 – 4000x + 20 x 2
⇔ 25 x 2 + 4000x – 200000 = 0 ⇔ x 2 + 160x – 8000 = 0
∆ ' = 80 2 – 1.(-8000) = 6400 + 8000 = 14400 > 0
∆ ' = 14400 = 120
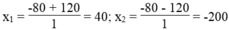
Giá trị x = -200 không thỏa mãn điều kiện bài toán.
Vậy số trứng của người thứ nhất là 40 quả
số trứng của người thứ hai là 100 – 40 = 60 quả.

Gọi số trứng của người thứ nhất là \(x\) (quả), \(x\in N^{\circledast},x< 100\)
Số trứng của người thứ hai là \(100-x\) (quả)


1/ Gọi năng suất, thời gian, số sản phẩm 2 người được giao là: x (sản phầm/h) , y (h), z (sản phẩm)
Người thứ nhất làm với năng suất: x + 1 nên ta có
\(\left(x+1\right)\left(y-2\right)=z\left(1\right)\)
Người thứ 2 làm với năng suất: x + 2 nên ta có
\(\left(x+2\right)\left(y-3\right)-7=z\left(2\right)\)
Năng suất đự định làm là: x nên ta có
\(xy=z\left(3\right)\)
Từ (1), (2), (3) ta có hệ: \(\hept{\begin{cases}\left(x+1\right)\left(y-2\right)=z\\\left(x+2\right)\left(y-3\right)-7=z\\xy=z\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=9\\y=20\\z=180\end{cases}}\)
2/ a/ Gọi số chim sẻ chim ngói và bồ câu mua là: x, y, z (con)
Giá 1 con chim sẻ là: \(\frac{1}{3}\)đồng
Giá 1 con chim ngói: \(\frac{1}{2}\)đồng
Giá 1 con chim bồ câu: 2 đồng
Ta có tổng số chim là 30 nên: x + y + z = 30
Tổng số tiền mua là 30 nên: \(\frac{x}{3}+\frac{y}{2}+2z=30\)
Từ đây ta có hệ: \(\hept{\begin{cases}x+y+z=30\\\frac{x}{3}+\frac{y}{2}+2z=30\end{cases}\Leftrightarrow}\hept{\begin{cases}x+y+z=30\\2x+3y+12z=180\end{cases}}\)
\(\hept{\begin{cases}x+y+z=30\left(1\right)\\y+10z=120\left(2\right)\end{cases}}\)
Xét (2) ta có: \(y+10z=120\)
\(y=120-10z\)
Mà \(1\le y\le30\)
\(\Rightarrow1\le120-10z\le30\Leftrightarrow9\le z\le11\)
Thế vô tìm được \(\left(x,y,z\right)=\left(0,20,10;9,10,11\right)\)
gọi x là số tiền của tôi lúc đầu
y là số tiền của bạn lúc đầu
ta có: x+1000=2(y-1000) => x=2y-3000(1)
x-1000=y+1000=>x=y+2000(2)
từ (1)(2)=>2y-3000=y+2000=>y-3000=2000=>y=5000
vậy số tiền của bạn lúc đầu là 5000
số tiền của tôi lúc đầu là x=5000+2000=7000