Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Gọi x (quả) là số trứng của người thứ nhất.
Điều kiện: x ∈N*, x < 100
Khi đó số trứng của người thứ hai là 100 – x (quả)
Giá tiền một quả trứng của người thứ nhất là 15/(100 - x) (đồng)
Giá tiền một quả trứng của người thứ hai là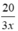 
(đồng)
Số tiền người thứ nhất bán được là:
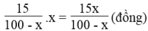
Số tiền người thứ hai bán được là:
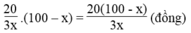
Theo đề bài, ta có phương trình:
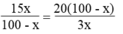
⇔ 45 x 2 = 20 100 - x 2 ⇔ 45 x 2 = 20(10000 – 200x + x 2 )
⇔ 45 x 2 = 200000 – 4000x + 20 x 2
⇔ 25 x 2 + 4000x – 200000 = 0 ⇔ x 2 + 160x – 8000 = 0
∆ ' = 80 2 – 1.(-8000) = 6400 + 8000 = 14400 > 0
∆ ' = 14400 = 120
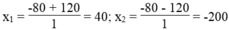
Giá trị x = -200 không thỏa mãn điều kiện bài toán.
Vậy số trứng của người thứ nhất là 40 quả
số trứng của người thứ hai là 100 – 40 = 60 quả.
Gọi số trứng của người thứ nhất là X.
Số trứng của người thứ hai là 100-X
Theo giải thiết ta có :
Trứng của người thứ nhất có giá là : 90000/100-X
Trứng của người thứ hai có giá là : 40000/X
Ta có hệ phương trình:
(90000/100-X)X=(40000/X)(100-X)
Giải hệ phương trình ta có:
X1=40
X2=-200 (loại)
Gọi a : tiền bán 1 quả trứng buổi sáng (a>0)
b : tiền bán 1 quả trứng buổi chiều (b>0)
x : số trứng bán được buổi sáng ( x ∈ N* )
y : số trứng bán được buổi chiều ( y ∈ N* )
Ta có hệ pt :
\(\left\{{}\begin{matrix}x+y=100\left(1\right)\\ax=by\left(2\right)\\ay=180\left(3\right)\\bx=80\left(4\right)\end{matrix}\right.\)
từ (2) ta có \(\dfrac{a}{b}=\dfrac{y}{x}\)
lấy (3) chia (4) ta được
\(\dfrac{ay}{bx}=\dfrac{180}{80}\)
thế \(\dfrac{a}{b}=\dfrac{y}{x}\) và ta được
\(\dfrac{y^2}{x^2}=\dfrac{9}{4}\)
⇔ y=\(\dfrac{3x}{2}\)
Thay y=\(\dfrac{3x}{2}\) vao (1)
Suy ra x=40;y=60
Vậy buổi sáng bán được 40 trứng, buổi chiều bán 60 trứng
Gọi số trứng của người thứ nhất là \(x\) (quả), \(x\in N^{\circledast},x< 100\)
Số trứng của người thứ hai là \(100-x\) (quả)
60 quả ở đâu đấy ạ