
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


`1)\sqrt{50}-3\sqrt{8}+\sqrt{32}=5\sqrt{2}-6\sqrt{2}+4\sqrt{2}=3\sqrt{2}`
`2)`
`a)\sqrt{x^2-4x+4}=1`
`<=>\sqrt(x-2)^2}=1`
`<=>|x-2|=1`
`<=>[(x-2=1),(x-2=-1):}<=>[(x=3),(x=1):}`
`b)\sqrt{x^2-3x}-\sqrt{x-3}=0` `ĐK: x >= 3`
`<=>\sqrt{x}\sqrt{x-3}-\sqrt{x-3}=0`
`<=>\sqrt{x-3}(\sqrt{x}-1)=0`
`<=>[(\sqrt{x-3}=0),(\sqrt{x}-1=0):}`
`<=>[(x-3=0),(\sqrt{x}=1):}<=>[(x=3(t//m)),(x=1(ko t//m)):}`

Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{3}{2}\\x_1x_2=-\dfrac{7}{2}\end{matrix}\right.\)
\(A=x_1^2+x_2^2=\left(x_1+x_2\right)^2-2x_1x_2=\dfrac{37}{4}\)
\(B=x_1^3+x_2^3=\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)=\dfrac{153}{8}\)
\(C=x_1^4+x_2^4=\left(x_1^2+x_2^2\right)^2-2\left(x_1x_2\right)^2=\dfrac{977}{16}\)
\(D=\left|x_1-x_2\right|=\sqrt{\left(x_1-x_2\right)^2}=\sqrt{\left(x_1+x_2\right)^2-4x_1x_2}=\dfrac{\sqrt{65}}{2}\)
\(E=\left(2x_1+x_2\right)\left(2x_2+x_1\right)=2\left(x_1^2+x_2^2\right)+5x_1x_2=1\)

`a,` Đthang đi qua `A(3, 12)`.
`-> x = 3, y = 12 in y`.
`<=> 12 = 9a.`
`<=> a = 12/9 = 4/3.`
`b,` Đthang đi qua `B(-2;3)`.
`=> x = -2, y = 3 in y`.
`<=> 3=4a`.
`<=> a = 3/4`.

`3x^2+10x+3=0`
Ptr có: `\Delta'=5^2-3.3=16 > 0`
`=>` Ptr có `2` nghiệm pb
`=>` Áp dụng Viét có: `{(x_1+x_2=[-b]/a=-10/3),(x_1 .x_2=c/a=1):}`
~~~~~~~~~~~~~
`A=x_1 ^2+x_2 ^2`
`A=(x_1+x_2)^2-2x_1 .x_2`
`A=(-10/3)^2-2.1=82/9`
_______________________________________________________
`B=x_1 ^3+x_2 ^3`
`B=(x_1+x_2)(x_1 ^2-x_1 .x_2+x_2 ^2)`
`B=(x_1+x_2)[(x_1+x_2)^2 -3x_1 .x_2]`
`B=(-10/3).[(-10/3)^2-3.1]=-730/27`
_______________________________________________________
`C=x_1 ^4+x_2 ^4`
`C=(x_1 ^2+x_2 ^2)^2 -2x_1 ^2 .x_2 ^2`
`C=[(x_1+x_2)^2-2x_1 .x_2]^2-2(x_1 .x_2)^2`
`C=[(-10/3)^2-2.1]^2-2. 1^2=6562/81`
_______________________________________________________
`D=|x_1-x_2|`
`D=\sqrt{(x_1-x_2)^2}`
`D=\sqrt{(x_1+x_2)^2-4x_1.x_2}`
`D=\sqrt{(-10/3)^2-4.1}=8/3`
_______________________________________________________
`E=(2x_1+x_2)(2x_2+x_1)`
`E=4x_1 .x_2+2x_1 ^2+2x_2 ^2+x_1 .x_2`
`E=5x_1 . x_2+2(x_1+x_2)^2-4x_1 .x_2`
`E=x_1 .x_2+2(x_1+x_2)^2`
`E=1+2(-10/3)^2=209/9`

\(A=\dfrac{\sqrt{x}+1+1}{\sqrt{x}+1}=1+\dfrac{1}{\sqrt{x}+1}>=1>0\)
=>A>|A|
Ta có: A= \(\dfrac{\sqrt{x}+2}{\sqrt{x}+1}\)= \(1+\dfrac{1}{\sqrt{x}+1}\)
Vì x ≥0⇒\(\sqrt{x}\) ≥0⇒\(\sqrt{x}+1 \)≥ 1 ⇒ \(1+\dfrac{1}{\sqrt{x}+1}\)≥ 2
hay A≥ 2>0
Khi đó ta có: A=|A|
Vậy A=|A|

a.
Phương trình hoành độ giao điểm (P) và (d):
\(\dfrac{1}{2}x^2=-\dfrac{3}{2}x+2\Leftrightarrow x^2+3x-4=0\)
\(\Rightarrow\left[{}\begin{matrix}x=1\Rightarrow y=\dfrac{1}{2}\\x=-4\Rightarrow y=8\end{matrix}\right.\)
Vậy (P) và (d) cắt nhau tại 2 điểm có tọa độ là \(\left(1;\dfrac{1}{2}\right)\) và \(\left(-4;8\right)\)
b.
Phương trình hoành độ giao điểm:
\(\dfrac{1}{2}x^2=mx+2\Leftrightarrow x^2-2mx-4=0\) (1)
\(ac=-4< 0\) nên (1) luôn có 2 nghiệm trái dấu
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2m\\x_1x_2=-4\end{matrix}\right.\)
Đặt \(P=x_1^2+x_2^2=\left(x_1+x_2\right)^2-2x_1x_2=4m^2+8\)
Do \(m^2\ge0;\forall m\Rightarrow2m^2+8\ge8;\forall m\)
\(\Rightarrow P_{min}=8\)
Dấu "=" xảy ra khi \(m^2=0\Rightarrow m=0\)
a: Khi m=-3/2 thì y=-3/2x+2
PTHĐGĐ là:
1/2x^2+3/2x-2=0
=>x^2+3x-4=0
=>(x+4)(x-1)=0
=>x=-4 hoặc x=1
=>y=1/2*(-4)^2=8 hoặc y=1/2
b: PTHĐGĐ là:
1/2x^2-mx-2=0
=>x^2-2mx-4=0
\(\Delta=\left(-2m\right)^2-4\cdot1\cdot\left(-4\right)=4m^2+16>0\)
=>PT luôn có hai nghiệm phân biệt
x1^2+x2^2
=(x1+x2)^2-2x1x2
=(2m)^2-2*(-4)=4m^2+8>=8
Dấu = xảy ra khi m=0

a. Em tự giải
b.
Phương trình hoành độ giao điểm (P) và (d):
\(-x^2=x+m-1\Leftrightarrow x^2+x+m-1=0\) (1)
(d) cắt (P) tại 2 điểm phân biệt khi và chỉ khi (1) có 2 nghiệm phân biệt
\(\Leftrightarrow\Delta=1-4\left(m-1\right)>0\Rightarrow m< \dfrac{5}{4}\)
Khi đó theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-1\\x_1x_2=m-1\end{matrix}\right.\)
\(4\left(\dfrac{1}{x_1}+\dfrac{1}{x_2}\right)+x_1x_2+3=0\)
\(\Leftrightarrow\dfrac{4\left(x_1+x_2\right)}{x_1x_2}+x_1x_2+3=0\)
\(\Leftrightarrow\dfrac{-4}{m-1}+m-1+3=0\)
\(\Rightarrow-4+\left(m-1\right)\left(m+2\right)=0\) (\(m\ne1\))
\(\Leftrightarrow m^2+m-6=0\Rightarrow\left[{}\begin{matrix}m=2>\dfrac{5}{4}\left(loại\right)\\m=-3\end{matrix}\right.\)
Vậy \(m=-3\)
a:
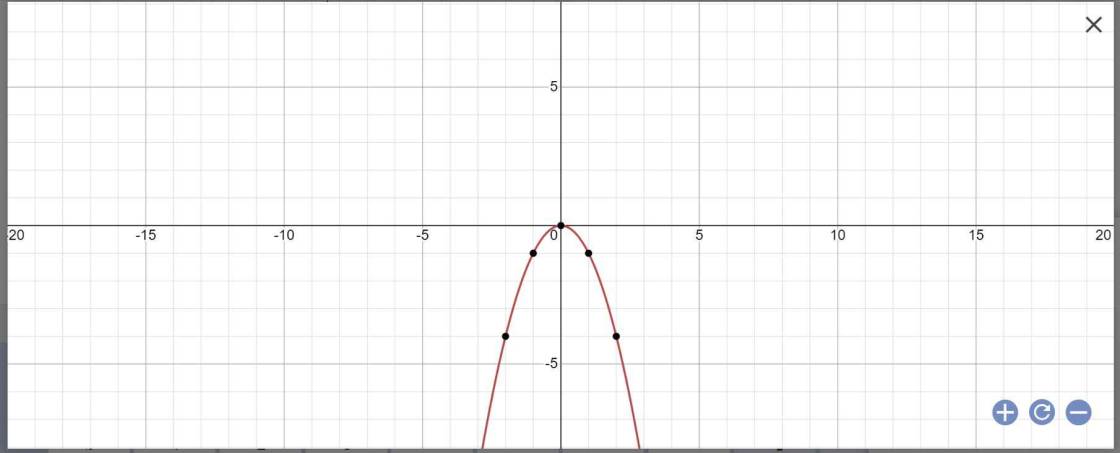
b: PTHĐGĐ là:
-x^2=x+m-1
=>-x^2-x-m+1=0
=>x^2+x+m-1=0
\(\Delta=1^2-4\left(m-1\right)=1-4m+4=5-4m\)
Để (P) cắt (d) tại hai điểm phân biệt thì 5-4m>0
=>4m<5
=>m<5/4
\(4\left(\dfrac{1}{x_1}+\dfrac{1}{x_2}\right)+x_1x_2+3=0\)
=>\(4\cdot\dfrac{x_1+x_2}{x_1x_2}+x_1x_2+3=0\)
=>\(4\cdot\dfrac{-1}{m-1}+m-1+3=0\)
=>-4+(m-1)^2+3(m-1)=0
=>(m-1+4)(m-1-1)=0
=>(m+3)(m-2)=0
=>m=2(loại) hoặc m=-3

Câu 11:
PTHĐGĐ là:
x^2-x-m+1=0
\(\Delta=\left(-1\right)^2-4\left(-m+1\right)=1+4m-4=4m-3\)
Để (P) cắt (d) tại hai điểm phân biệt thì 4m-3>0
=>m>3/4
|x1-x2|=2
=>\(\sqrt{\left(x_1+x_2\right)^2-4x_1x_2}=2\)
=>\(\sqrt{1^2-4\left(-m+1\right)}=2\)
=>1+4m-4=4
=>4m-3=4
=>m=7/4
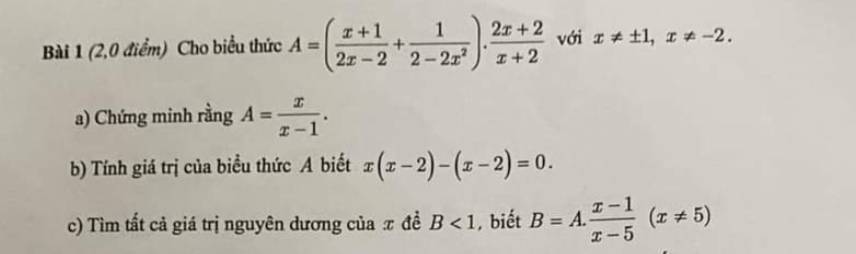

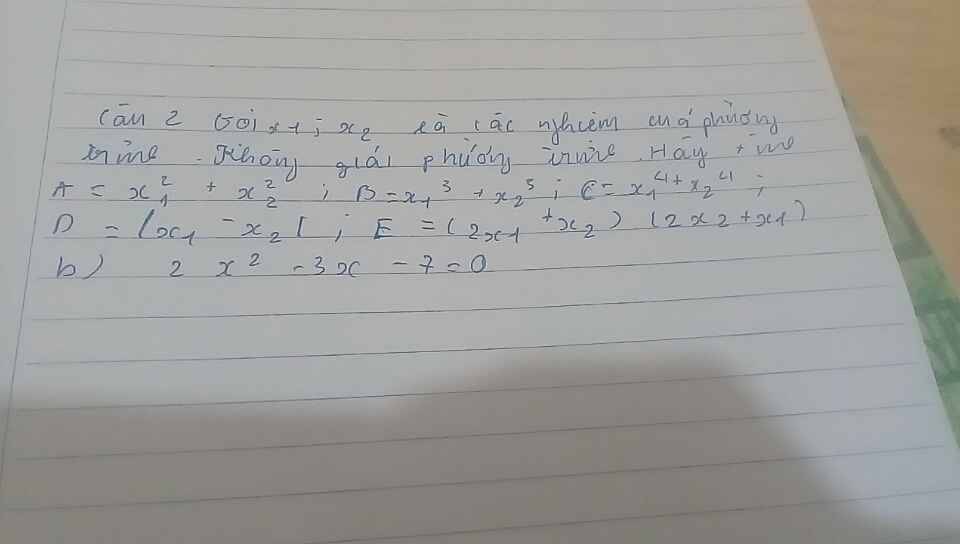
 giup minh cau nay voi
giup minh cau nay voi

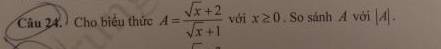

 giup minh cau nay voi
giup minh cau nay voi giup minh cau nay voi
giup minh cau nay voi
a: \(A=\dfrac{x^2+2x+1-1}{2\left(x-1\right)\left(x+1\right)}\cdot\dfrac{2\left(x+1\right)}{x+2}\)
\(=\dfrac{x\left(x+2\right)}{2\left(x-1\right)}\cdot\dfrac{2}{x+2}=\dfrac{x}{x-1}\)
b: x(x-2)-(x-2)=0
=>(x-2)(x-1)=0
=>x=2(nhận) hoặc x=1(loại)
Khi x=2 thì A=2/(2-1)=2