

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



+ Khi \(W_đ=3W_t\Rightarrow W=4W_t\Rightarrow x=\pm\frac{A}{2}\)
+ Khi \(W_đ=\frac{1}{3}W_t\Rightarrow W=\frac{4}{3}W_t\Rightarrow x=\pm\frac{\sqrt{3}}{2}A\)
Ta có véc tơ quay như sau:
Thời gian nhỏ nhất ứng với véc tơ quay từ M đến N.
\(t=\frac{30}{360}T=\frac{1}{12}.2=\frac{1}{6}s\)
\(S=\left(\frac{\sqrt{3}}{2}-\frac{1}{2}\right).10=\left(\sqrt{3}-1\right).5\)
Tốc độ trung bình: \(v=\frac{S}{t}=\left(\sqrt{3}-1\right).30=21,96\)(cm/s)

Chọn đápán D.
![]()
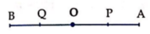
Giả sử vật dao động điều hòa quanh VTCB O, với A, B là các vị trí biên.
Gọi P, Q là các điểm mà tại đó tốc độ của vật bằng v 0 thì P, Q sẽ đối xứng nhau qua O. Khi vật chuyển động giữa hai điểm P, Q thì tốc độ của vật lớn hơn v 0 .
Trong một chu kì thời gian vật chuyển động với tốc độ lớn hơn v 0 sẽ bằng 2 lần thời gian vật chuyển động từ P đến Q.
Suy ra, thời gian vật chuyển động từ p đến Q là t P Q = 1 / 2 s
Mà theo đề bài, tốc độ trung bình khi vật chuyển động từ P đến Q là v P Q = 20 c m / s .
Do đó P Q = v P Q . t P Q = 10 c m
Suy ra, P là trung điểm của OA và x P = 5 c m .
Mà thời gian vật chuyển động từ P đến O là T/12
nên ta có T 12 = 1 2 t P Q ⇒ T = 6 t P Q = 3 s ⇒ ω = 2 π T = 2 π 3
Từ đó áp dụng công thức độc lập theo thời gian ta có tốc độ v 0 của vật là
v 0 = ω A 2 − x 2 = 2 π 3 10 2 − 5 2 = 10 π 3 ≈ 18 , 1 cm/s

Đáp án D
Giả sử vật dao động điều hòa quanh VTCB O, với A, B là các vị trí biên.
Gọi P, Q là các điểm mà tại đó tốc độ của vật bằng v0 thì P, Q sẽ đối xứng nhau qua O. Khi vật chuyển động giữa hai điểm P, Q thì tốc độ của vật lớn hơn v0 sẽ bằng 2 lần thời gian vật chuyển động từ P đến Q.
Suy ra, thời gian vật chuyển động từ P đến Q là t PQ = 1 2 s
Mà theo đề bài, tốc độ trung bình khi vật chuyển động từ P đến Q là
v PQ = 20 cm / s
 Do đó
PQ
=
v
PQ
.
t
PQ
=
10
cm
Do đó
PQ
=
v
PQ
.
t
PQ
=
10
cm
Suy ra, P là trung điểm của OA và x P = 5 cm
Mà thời gian vật chuyển động từ P đến O là T/12 nên ta có
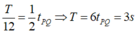
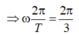
Từ đó áp dụng công thức độc lập theo thời gian ta có tốc độ v0 của vật là
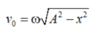
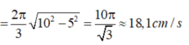

Đáp án B
Phương pháp: Áp dụng hệ thức độc lập với thời gian của vận tốc và li độ
Cách giải:
Tần số góc: ω = 2π/T = π (rad/s)
Tốc độ của vật khi cách VTCB 6cm:
![]()
![]()
=> Chọn B

\(v=\omega\sqrt{A^2-x^2}=\dfrac{2\pi}{T}\sqrt{A^2-x^2}=5\pi\sqrt{3}\left(cm.s^{-1}\right)\)