Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ban đầu vật ở vị trí có pha ban đầu là -pi/3
Sau 13s, vật quét được góc: \(\varphi=\omega t=4\pi.13=52\pi\left(rad\right)\)
Vì góc quay được chia hết cho 2, nghĩa là sau 13s, vật sẽ quay về vị trí ban đầu có pha là -pi/3
\(\Rightarrow S=45cm=3+7.6=\dfrac{A}{2}+7A\)
Vậy vật quay được góc: \(\varphi=\dfrac{\pi}{3}+4\pi-\dfrac{\pi}{2}=\dfrac{23}{6}\pi\left(rad\right)\)
\(\Rightarrow t=\dfrac{\varphi}{\omega}=\dfrac{23\pi}{6.4\pi}=\dfrac{23}{24}\left(s\right)\)

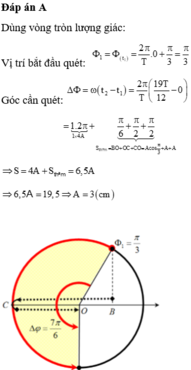
Đáp án A
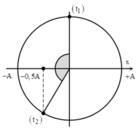
+ Tại thời điểm t = 0 vật đi qua vị trí cân bằng theo chiều âm.
→ Khoảng thời gian Δt tương ứng với góc quét Δφ = ωΔt = π 2 3 = 2 π 3 rad.
→ Thời điểm t 2 vật đến vị trí có li độ x = – 0,5A theo chiều dương.
+ Quãng đường vật đi được là S = A + 0,5A = 1,5A.

S=30=20+10=T/2+T/6=2T/3
T=2pi/pi=2
=> thời gian = 2*2/3=4/3s

S=5cm= 4+1= T+T/6 = 7T/6( do cung ban đầu là 2pi/3, do A=1 nên T=4)
\(T=\dfrac{2\pi}{\omega}=\dfrac{2\pi}{\pi}=2\)
thời gian đi được = 7*2/6=7/3s.

Đáp án D
Phương pháp: Sử dụng đường tròn lượng giác
Ta có T = 0,4s => t = 11T + T/4
Ta thấy vật sẽ đi được 11 chu kì và trở về vị trí cũ rồi thực hiện được ¼ chu kì nữa như hình vẽ:
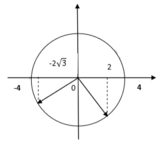
Quãng đường vật đi được sau khoảng thời gian t = 4,5s là:
![]()

Nghĩa là nó sẽ đi một lần A/2, 1 lần A, và 1 lần A/3
\(\Rightarrow\varphi=\dfrac{\pi}{3}+\dfrac{\pi}{2}+\dfrac{\pi}{2}-arc\cos\left(\dfrac{1}{3}\right)=...\left(rad\right)\)
\(\Rightarrow t=\dfrac{\varphi}{\omega}=\dfrac{\varphi}{3\pi}\left(s\right)\)