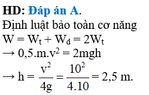Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A. Định luật bảo toàn cơ năng
W = W t + W d = 2 W t ⇒ 1 2 m v 2 = 2 m g h ⇒ h = v 2 4 g = 10 2 4.10 = 2 , 5 m

a, \(W_đ=\dfrac{1}{2}mv^2=\dfrac{1}{2}\cdot0,1\cdot5^2=1,25\left(J\right)\)
\(W_t=mgz=0,1\cdot10\cdot2=2\left(J\right)\)
\(W=W_đ+W_t=1,25+2=3,25\left(J\right)\)
b, Gọi vị trí 1 là vị trí vật đạt được độ cao cực đại
Khi vật đạt được độ cao cực đại z1 thì v1 = 0
\(W_1=W_{đ_1}+W_{t_1}=\dfrac{1}{2}mv_1^2+mgz_1=mgz_1\)
Áp dụng ĐLBTCN: \(W=W_1\Leftrightarrow W=mgz_1\Leftrightarrow z_1=\dfrac{W}{mg}=\dfrac{3,25}{0,1\cdot10}=3,25\left(m\right)\)

huhu sao hôm nay box lý nhiều bài tập quá vậy :(
a) \(W_đ=\dfrac{1}{2}mv_0^2=25\left(J\right)\) \(W_t=mgh=100\left(J\right)\)
\(W=W_đ+W_t=\dfrac{1}{2}mv_0^2+mg.20=125\left(J\right)\)
b) :D không biết cái công thức này mình chứng minh tổng quát bao nhiêu lần rồi?
chọn trục Ox thẳng đứng, hướng lên, Gốc O tại điểm ném gốc thời gian t=0
Xét tại thời điểm ném: \(\left\{{}\begin{matrix}v=v_0-gt\\x=v_0t-\dfrac{1}{2}gt^2\end{matrix}\right.\) tại điểm cao nhất của vật có nghĩa là v=0
Từ đây suy ra \(x=h_{max}=\dfrac{v_0^2}{2g}\) => độ cao lớn nhất vật đạt đc: h=20+5=25(m)
c) Khi chạm đất Bảo Toàn cơ năng:
\(W'=W_đ'+W_t'=\dfrac{1}{2}mv'^2=W=125\left(J\right)\)
\(\Rightarrow v'=10\sqrt{5}\left(m/s\right)\)
d) ở độ cao 5m so với mặt đất à bạn?
Bảo toàn cơ năng: \(W_1=W_2\Leftrightarrow\dfrac{1}{2}mv_1^2+mgh_1=\dfrac{1}{2}mv_2^2+mgh_2\) => v2=..... ( tự tính đi )
e) Cũng bảo toàn cơ năng nốt:
\(W=W'\) \(\Leftrightarrow\dfrac{1}{2}mv_1^2+mgh=3mgh'\) => h'=....
\(W=W'\Leftrightarrow\dfrac{1}{2}mv_1^2+mgh=\dfrac{3}{2}mv'^2\) => v'=
W với W' tùy từng câu mà thay số cho hợp lí nha bạn :D tại W vs W' có mấy chỗ bị trùng không rõ chỗ nào ib hỏi mình.
ở câu e tính vận tốc là 3/4mv'^2 nha không phải 3/2mv'^2 đâu mình quên nhân 1/2 :(

Chọn gốc thế năng tại độ cao 5m so với mặt đất.
\(\Rightarrow h=10-5=5cm\)
Cơ năng vật:
\(W=\dfrac{1}{2}mv^2+mgh=\dfrac{1}{2}\cdot0,4\cdot20^2+0,4\cdot10\cdot5=100J\)
Ta có
\(W=W_đ+W_t\\ \Leftrightarrow mgh+\dfrac{mv^2}{2}=0,4.10.10+\dfrac{0,4.20^2}{2}\\ =120\left(J\right)\)