Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

d = 20 mm = 20.10-3m
E = 2.1011 Pa
Fnén = 1,57.105 N
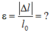
Ta có: 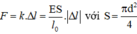
→ Độ biến dạng tỉ đối của thanh:
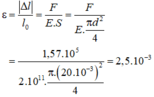

Đáp án: D
Lực nén vào thanh thép bằng đúng lực đàn hồi xuất hiện trong thanh.
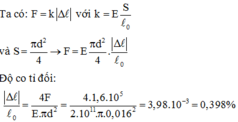

Ta có : F = k△l = \(\frac{E.S}{l_0}\). | △l |
→ \(\frac{\triangle l}{l_0}=\frac{F}{E.S}=\frac{157.10^3}{2.10^{11}.\left(10^{-2}\right)^2.3,14}=25.10^{-4}=0,25.10^{-2}\)
Vậy độ biến dạng tỉ đối của thanh là \(\frac{\triangle l}{l_0}=0,25.10^{-2}\)
@phynit
Em trả lời 100% . Không có sự tự hỏi tự trả lời đâu ạ ( Em nói để thầy biết và không nghĩ oan cho em )

Ta có : F = k\(\triangle\)l = \(\frac{E.S}{l_o}\). | \(\triangle\)l |
→ \(\frac{\triangle l}{l_0}=\frac{F}{E.S}=\frac{157.10^3}{2.10^{11}.\left(10^{-2}\right)^2.3,14}\)= 25 . 10-4 = 0,25 .10-2
Vậy độ biến dạng tỉ đối của thanh là \(\frac{\triangle l}{l_0}\)= 0,25 . 10-2

Đáp án: D
Lực nén vào thanh thép bằng đúng lực đàn hồi xuất hiện trong thanh.
Ta có:
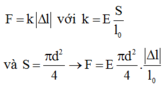
Độ co tỉ đối:
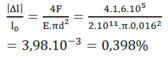

Chọn D
Lực nén vào thanh thép bằng đúng lực đàn hồi xuất hiện trong thanh.
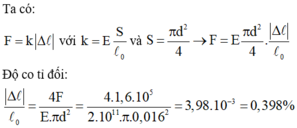

d = 20 mm
E = 2.1011 Pa
Fnén = 1,57.105 N
Tìm \(\varepsilon=\dfrac{\left|\Delta t\right|}{l_0}=?\)
Ta có: \(F=k\Delta l=\dfrac{ES}{l_0}\left|\Delta t\right|\)
\(\Rightarrow\dfrac{\Delta l}{l_0}=\dfrac{F}{ES}=25.10^4=0,25.10^{-2}\)
Vậy độ biến dạng tỉ đối của thanh là : \(\dfrac{\left|\Delta l\right|}{l_0}=2,5.10^{-3}\)

Chọn đáp án C
Khi bị nung nóng, độ dài của thanh đồng thau tăng, muốn giữ độ dài của thanh này không thay đổi, ta phải tác dụng lên hai đầu thanh một ứng suất nén sao cho độ biến dạng nén bằng độ nở dài vì nhiệt của nó
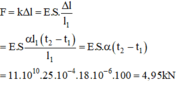

Ta có,
+ Lực nén đàn hồi: F d h = k . ∆ l = E S l 0 ∆ l (1)
+ Mặt khác, độ biến dạng tỉ đối được xác định: ε = ∆ l l 0 = α σ (2)
Từ (1) và (2), ta suy ra: ε = F d h E . S
Tiết diện của thanh: S = πr 2 = π d 2 4 = π 20 . 10 - 3 2 4 = π . 10 - 4 m 2
Thay vào (3), ta được: ε = F d h E . S = 3 , 14 . 10 5 2 . 10 11 . π . 10 - 4 ≈ 5 . 10 - 3
Đáp án: D
Chọn đáp án A
Hướng dẫn:
Áp dụng định luật Húc về độ biến dạng tỉ đối của vật rắn: