Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chiếu lên trục tọa độ Ox có phương trùng với phương mp nghiêng, chiều hướng xuống
Oy có phương vuông góc với mpn, chiều hướng lên
\(\Rightarrow\left\{{}\begin{matrix}Ox:mg\sin\alpha\ge\mu N\\Oy:N=mg\cos\alpha\end{matrix}\right.\Rightarrow mg\sin\alpha\ge\mu mg\cos\alpha\)
\(\Leftrightarrow\sin\alpha\ge\mu\cos\alpha\)
Chỗ bạn học giải bpt lượng giác chưa vậy?

Để xe nằm yên ko trượt đồng nghĩa với việc các lực t/d lên nó phải triệt tiêu nhau, nghĩa là: \(\overrightarrow{P}+\overrightarrow{F_{ms}}+\overrightarrow{N}=\overrightarrow{0}\)
\(\Rightarrow\left\{{}\begin{matrix}mg\sin\alpha=\mu N\\N=mg\cos\alpha\end{matrix}\right.\Rightarrow mg\sin\alpha=\mu mg\cos\alpha\)
\(\Leftrightarrow\sin\alpha=0,2\cos\alpha\)
Thấy cos alpha=0 ko là nghiệm của phương trình, chia 2 vế cho cos alpha \(\tan\alpha=0,2\Rightarrow\alpha=11^0\)

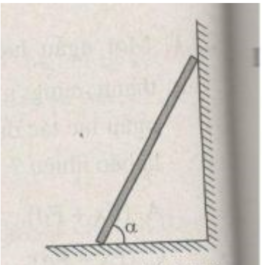
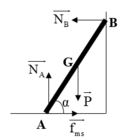
a. Trọng lượng của thanh: P = mg = 200N
Theo điều kiện cân bằng Momen
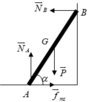
M P → = M N → B ⇒ P . A B 2 cos α = N B . A B . sin α
Theo điều kiện cân bằng lực
P → + N → A + N → B + F → m s = 0 → N A = P = 200 N ; F m s = N B ⇒ N B = F m s = P 2 = 100 N
b, Điều kiện: Fms <k.NA
Theo câu a F m s = N B = P 2 t g α
⇒ N A = P ⇒ t g α > 1 2 k = 1 1 , 2 ⇒ α = 40 0
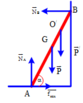
c. Lấy O’ là vị trí người khi thang bắt đầu trượt.
Ta có:
N B = F m s = k N A ; N A = P + P ' = 600 N F m s = 360 N
Xét trục quay qua A
M N → B = M P → + M P ' → N B . A B sin α = P . A B 2 . cos α + P ' . A O ' . cos α ⇒ A O ' = 1 , 3 m


Chọn A.
Trọng lượng của thanh: P = mg = 200N
Theo điều kiện cân bằng Momen:


Theo điều kiện cân bằng lực:

Để thang đứng yên không trượt trên sàn thì fms < k.NA.
![]()

Chọn B.
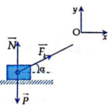
Áp dụng định luật II Niu-tơn:
![]()
Chiếu lên Oy: N = P – F.sinα
Chiếu lên Ox: F.cosα – μN = m.a
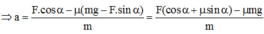
Theo Bất đẳng thức Bu-nhi-a - Cốp-xki:
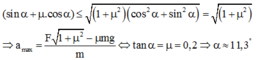




Chọn đáp án B