Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án B
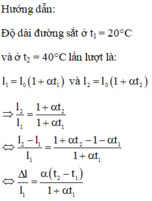
Vì α t 1 << 1 nên khi nhiệt độ tăng từ t 1 = 20 ° C đến t 2 = 40 ° C thì đoạn đường sắt này sẽ dài thêm một đoạn đường gần đúng bằng
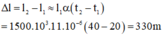

Áp dụng công thức về sự nở dài ta có:
\(l=l_0\left(1+\alpha\Delta t\right)\)
thay số :\(l=10\left(1+12\times10^{-6}\times\left(40-10\right)\right)=10,0036\left(m\right)\)
KL : vậy \(l=10,0036m\)

\(l_2=l_1\left(1+\alpha\Delta t\right)\Rightarrow\Delta l=l_2-l_1=l_1\alpha\Delta t\)
⇒ Δl = 25.11,8.10-6.(50-20) = 8,85.10-3m

Vì các thanh ray được đặt nối tiếp nhau, ở cả hai đầu thanh ray đều có khe hở và các thanh ray nở cả về hai đầu nên khe hở phải có độ rộng h tương ứng với độ nở dài của một thanh ray khi nhiệt độ tăng từ 25 ° C lên 60 ° C Áp dụng công thức: 1 = 1 0 ( 1 + α t )
![]()
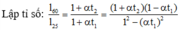
![]()
![]()
![]()

![]()

Đáp án: C
Vì các thanh ray được đặt nối tiếp nhau, ở cả hai đầu thanh ray đều có khe hở và các thanh ray nở cả về hai đầu nên khe hở phải có độ rộng h tương ứng với độ nở dài của một thanh ray khi nhiệt độ tăng từ 25 oC lên 60 oC.
Áp dụng công thức: l = l 0 ( l + α t ) (l0 là chiều dài ở 0 oC)
Ở 250C : l 25 = l 0 ( l + t 1 α ) và ở 600C : l 60 = l 0 ( l + t 2 α )
Lập tỉ số:

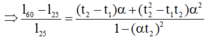
Thép làm thanh ray có α = 11 , 4 . 10 - 6 K - 1 n ê n α 2 ≪ 1 có thể bỏ qua.
Khi đó:
![]()
Thay số:
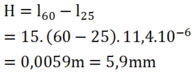

Chọn A
Vì các thanh ray được đặt nối tiếp nhau, ở cả hai đầu thanh ray đều có khe hở và các thanh ray nở cả về hai đầu nên khe hở phải có độ rộng h tương ứng với độ nở dài của một thanh ray khi nhiệt độ tăng từ 25 o C lên 60 o C

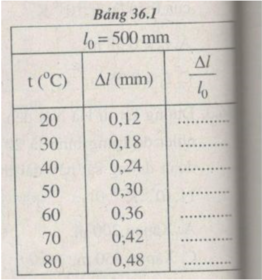
Hình 36.1G có dạng đoạn thẳng.
Điều này chứng tỏ độ biến dạng tỉ đối ∆ l/ l 0 của thanh sắt tỉ lệ thuận với độ tăng nhiệt độ t (tính từ 0 ° C):
∆ l/ l 0 = α t
Nhận xét thấy hệ số tỉ lệ α chính là hệ số nở dài của thép.
Hệ số tỉ lệ α được xác định bởi hệ số góc của đường biểu diễn đồ thị ở Hình 36.1G.

Khi nhiệt độ tăng từ 0 ° C đến t ° C thì độ dãn dài của :
- Thanh thép : ∆ l 1 = l 01 α 1 t.
- Thanh đồng : ∆ l 2 = l 02 α 2 t.
Từ đó suy ra độ dài chênh lệch của hai thanh thép và đồng ở nhiệt độ bất kì t ° C có giá trị bằng :
∆ l = ∆ l1 – ∆ l2 = l 01 α 1 t – l 02 α 2 t = ( l 01 α 1 – l 02 α 1 )t = 50 mm
Công thức này chứng tỏ ∆ l phụ thuộc bậc nhất vào t. Rõ ràng, muốn ∆ l không phụ thuộc t, thì hệ số của t phải luôn có giá trị bằng không, tức là :
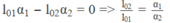
hay:
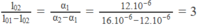
Từ đó suy ra độ dài ở 0 ° C của :
- Thanh đồng : l 02 = 3( l 01 - l 02 ) = ∆ l = 3.50 = 150 mm.
- Thanh thép : l 01 = l 02 + ∆ l = 150 + 50 = 200 mm.

Đáp án C