Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Nguồn điện có f = 50 Hz → tần số sóng trên dây là f = 100 Hz.
Sợi dây có hai đầu cố định → l = kλ/2; trên dây có 2 bụng sóng → k = 2.
→ λ = 1,2 m.
Tốc độ truyền sóng trên dây là v = λf = 1,2.100 = 120 m/s.
Theo em:
Hai đầu cố định: l=k\(\frac{_{ }\lambda}{2}\) => l=2.\(\frac{v}{2f}\) => 1.2=2.\(\frac{v}{2.50}\) => bấm shift solve ra = 60m/s
Đáp án D nhé

Đáp án B.
Bước sóng λ = v f = 25 c m
Điều kiện để có sóng dừng trên dây với hai đầu cố định là : I = n v 2 f ⇒ n = 2 I f v = 8
Vậy trên dây có sóng dừng với 8 bó sóng
Các bó sóng liên tiếp nhau sẽ dao động ngược pha nha
Vậy sẽ có 7 điểm dao động cùng biên độ và cùng pha với M

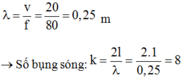
Mỗi bó sóng sẽ có 2 điểm cùng biên độ với M, các điểm cùng pha với nhau phải cùng nằm trên 1 bó hoặc các bó đối xứng qua một bụng nên nếu không tính điểm M sẽ có 7 điểm cùng biên độ và cùng pha với M.
Đáp án B

Đáp án C
+ Bước sóng của sóng λ = v f = 25 cm → trên dây có sóng dừng với 8 bóng sóng.
Mỗi bó sóng sẽ có 2 điểm cùng biên độ với M, các điểm cùng pha với nhau phải cùng nằm trên 1 bó hoặc các bó đối xứng qua một bụng → không tính M sẽ có 7 điểm cùng biên độ và cùng pha với M.

Chọn đáp án C
Điều kiện để có sóng dừng trên dây với hai đầu cố định: ![]() , với n là số bó sóng hoặc số bụng sóng
, với n là số bó sóng hoặc số bụng sóng
→
Thay các giá trị đã biết vào biểu thức: ![]()
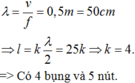



Đáp án C
Trên dây có sóng dừng với 3 bụng sóng → n = 3.
Điều kiện để có sóng dừng với hai đầu cố định l = 3 v 2 f ⇒ v = 2 l f 3 = 80 m / s