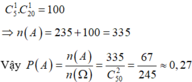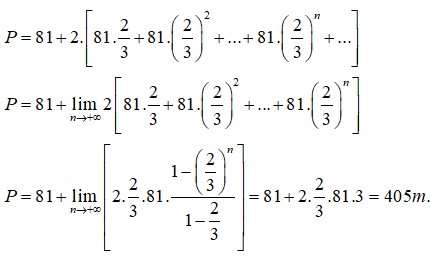Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Tổng khoảng cách cần tìm là (với n ∈ R * )
S
=
81
+
2
.
81
.
2
3
+
2
.
81
.
2
3
2
+
.
.
.
+
2
.
81
.
2
3
n
+
1
=
81
+
2
.
81
.
2
3
+
81
.
2
3
2
+
.
.
.
+
81
.
2
3
n
+
1
+
.
.
.
Do 81 . 2 3 + 81 . 2 3 2 + . . . + 81 . 2 3 n + 1 + . . . l
à tổng của cấp số nhân lùi vô hạn với
u 1 = 81 . 2 3 = 54 q = 2 3 ⇒ S = 81 + 2 . u 1 1 - q = 405 m

Đáp án C
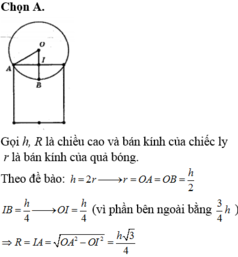
Gọi S là tổng quãng đường bóng đã bay, khi đó ta có:
S = 3 + 3. 2 3 .3 2 3 2 + 3. 2 3 3 + 3. 2 3 4 + 3. 2 3 5 + ... + 3. 2 3 n + ...
S là tổng của cấp số nhân lùi vô hạn có số hạng đầu tiên là u 1 = 3 , công bội là q = 2 3 nên
S = u 1 1 − q = 3 1 − 2 3 = 9
Vậy tổng quãng đường đã bay của bóng là khoảng 9m.

Đáp án C
Phương pháp:
Chia thành các trường hợp:
+ Trong hai quả bóng bốc được có ít nhất một quả có số chia hết cho 10.
+ Trong hai quả bốc được có một quả có chữ số hàng đơn vị bằng 5 và một quả có chữ số hàng đơn vị là 2,4,6,8.
Đếm số khả năng có lợi cho biến cố và tính xác suất.
Cách giải:
Xét phép thử T: “Bốc ngẫu nhiên 2 trong 50 quả bóng”.
Số phần tử không gian mẫu n Ω = C 50 2
Gọi A là biến cố: “Tích hai số ghi trên hai bóng chia hết cho 10:.
+) TH1: Trong hai quả bốc được có ít nhất 1 quả có số chia hết cho 10
Số cách chọn để trong hai quả không có quả nào có số chia hết cho 10 là C 45 2
→ Số cách chọn để trong hai quả có ít nhất 1 quả có số chia hết cho 10 là
![]()
+) TH2: Trong hai quả bốc được có 1 quả có chữ số hàng đơn vị là 5 và 1 quả có chữ số hàng đơn vị là 2,4,6,8.
Số cách chọn để có được hai số trên (không phân biệt thứ tự) là