Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Ta có : 2 B C - A B ≤ 2 m
Mặt khác : B C . A B = 20 m (1)
Công suất lớn nhất khi B C m a x ⇒ 2 B C - A B = 2 m (2)
Từ (1) và (2) suy ra : B C ≈ 3 , 7 m ; A B ≈ 5 , 4 m
Dễ dàng tính được : AM = 4,58m và A’M = 6,08m
Tại người nghe được âm có mức cường độ âm lớn nhất là 13(B) = 130(dB)
⇒ 13 = log ( 2 P 4 π A M 2 I 0 + 2 P 4 π A ' M 2 I 0 ) ⇒ P = 840 , 9 ( W ) .

Đáp án C
Cường độ âm do các loa truyền đến điểm M :
I M = ( I N + I N ' ) ≡ P 2 π 1 a 2 + b 2 4 + 1 a 2 + b 2 4 + h 2
Để IM là lớn nhất thì biểu thức dưới mẫu phải nhỏ nhất. Ta có :
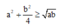 dấu bằng xảy ra khi
a
=
b
2
⇒
a
=
3
b
=
6
dấu bằng xảy ra khi
a
=
b
2
⇒
a
=
3
b
=
6
Giá trị cường độ âm khi đó
( I M ) m a x = 5 P m a x 108 π = 10
⇒ P m a x = 678 W

Đáp án A
Để người ngối ở tâm nhà nghe rõ như 4 loa đặt ở góc tường thì cường độ âm do các loa nhỏ gây ra ở tâm bằng cường độ âm do loa ban đầu gây ra ở tâm nhà.
I = P 0 4 π R 2 = n P 4 π R 2 4
Với P 0 = 8 P , R là khoảng cách từ tâm nhà đến góc tường → 4n = 8 → n = 2.

Cường độ âm I' ứng với mức 70 dB hay 7 B là :
I ' = 10 I 0 = 10 7 . 10 - 12 = 10 - 5 w / m 2
Vây phải giảm nhỏ công suất của loa : N = 5. 10 - 3 / 10 - 5 = 500 lần.

Tại điểm cách loa 1m ta có \(R=1m\)
Cường độ âm có độ lớn:
\(I=\dfrac{P}{4\pi R^2}=\dfrac{1}{4\pi\cdot1^2}=\dfrac{1}{4\pi}\approx0,08W/m^2\)

Chọn B.
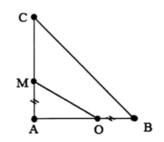
Δ A B C vuông cân tại A: C B = A B 2
Ta có: M O 2 = A M 2 + A O 2 = A M 2 + A B − O B 2
= A M 2 + A B 2 + O B 2 − 2 A B . O B
Mà OB = AM nên:
M O 2 = 2 A M 2 − 2 A M . A B + A B 2 = 2 A M − A B 2 2 + A B 2 2 ≥ A B 2 2
Dấu “=” xảy ra khi OM nhỏ nhất hay mức cường độ âm tại M lớn nhất
⇒ M O min = A B 2 = C B 2
L − C L M = log M O C B 2 ⇔ 4 − L M = log 1 4 ⇒ L M = 4,6 B = 46 d B .
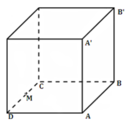
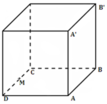


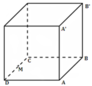
- Ta có : 2BC - AB ≤ 2m.
- Mặt khác: BC.AB = 20m (1)
- Công suất lớn nhất khi:
BCmax ⇒ 2BC - AB = 2m (2)
- Từ (1) và (2) suy ra :
BC ≈ 3,7m; AB ≈ 5,4m.
- Dễ dàng tính được :
AM = 4,58m và A’M = 6,08m
- Tại người nghe được âm có mức cường độ âm lớn nhất là 13(B) = 130(dB):