Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tốc độ góc ω và gia tốc hướng tâm a h t của một điểm trên vành ngoài của bánh xe có bán kính r = 25 cm = 0,25 m khi ô tô đang chạy với tốc độ dài v = 36 km/h = 10 m/s bằng
ω = v/r = 10/0.25 = 40 (rad/s)
a h t = v 2 /r = 10 2 /0.25 = 400 (m/ s 2 )

Bánh xe quay đều với tốc độ góc ω = 2π (rad/s).
Do đó một điểm M thuộc vành ngoài bánh xe cũng quay đều với cùng tốc độ góc ω = 2π (rad/s).
Chu kỳ quay của M: T = 2π/ω = 1 (s).
Tần số quay của M: f = 1/T = 1 Hz.
Tốc độ dài của M: v = R.ω = 0,3.2π = 0,6π (m/s) ≈ 1,9 (m/s).
Gia tốc hướng tâm của M: an = R.ω2 = 0,3.(2π)2 = 12 m/s2.

Gia tốc hướng tâm 1 điểm trên vành bánh xe:
\(a_{ht}=\dfrac{v^2}{r}=\dfrac{10^2}{0,5}=200\) m/s2
Gia tốc hướng tâm tại 1 điểm cách vành bánh xe 10cm:
\(a_{ht}=\dfrac{v^2}{r'}=\dfrac{10^2}{0,1}=1000\) m/s2

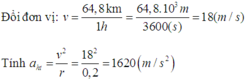
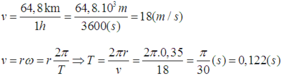

R=30cm=0,3m
v=64,8km/h=18m/s
Tốc độ góc của 1 điểm trên vành ngoài bánh xe:
\(\text{ω}=\dfrac{v}{R}=\dfrac{18}{0,3}=60\) (rad/s)
Chu kì quay của bánh xe:
\(T=\dfrac{2\text{π}}{\text{ω}}=\dfrac{2\text{π}}{60}=\dfrac{\text{π}}{30}\) (s)
Gia tốc hướng tâm của điểm đó:
\(a_{ht}=\text{ω}^2R=60^2.0,3=1080\) (m/s2)