Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi x (km/h) là vận tốc lúc về. Điều kiện: x > 0
Ta có vận tốc lúc đi là x + 10 (km/h)
Thời gian lúc đi là 150/(x + 10) (giờ)
Thời gian lúc về là 150/x (giờ)
Thời gian nghỉ là 3 giờ 15 phút = 3.(1/4) (giờ) = 13/4 (giờ)
Theo đề bài, ta có phương trình:
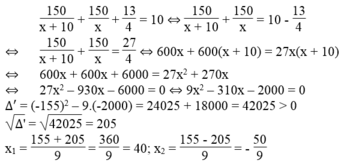
Giá trị x = - 50/9 không thỏa mãn điều kiện bài toán.
Vậy vận tốc ô tô lúc về là 40km/h.

Gọi quãng đường từ Hà Nội đến Đền Hùng là a(km) \(\left(a>0\right)\)
\(\Rightarrow\) thời gian đi là \(\dfrac{a}{30}\) (h)
Theo đề: vận tốc lúc về là \(30+10=40\) (km/h)
\(\Rightarrow\) thời gian về là \(\dfrac{a}{40}\) (h)
36 phút = \(\dfrac{3}{5}\) (h)
Theo đề: \(\dfrac{a}{40}+\dfrac{3}{5}=\dfrac{a}{30}\Rightarrow\dfrac{a+24}{40}=\dfrac{a}{30}\Rightarrow30a+720=40a\)
\(\Rightarrow10a=720\Rightarrow a=72\) (km)
Gọi quãng đường từ Hà Nội đến Đền Hùng là
Vận tốc của ô tô khi đi từ Đền Hùng về Hà Nội là:
Thời gian ô tô đi từ Hà Nội đến Đền Hùng là
Thời gian ô tô đi từ Đền Hùng về Hà Nội là
phút
Vì thời gian về rút ngắn hơn thời gian đi là phút nên ta có :
Vậy ...

Để giải hệ phương trình theo phương pháp thế, ta cần tìm ra 2 biến là vận tốc dự định (v1) và vận tốc tăng thêm (v2) sau khi nghỉ 30 phút.
Quãng đường đi đầu tiên: 120km / 2 = 60kmThời gian đi đầu tiên: 60km / v1 = t1Quãng đường đi thứ hai: 120km - 60km = 60kmThời gian đi thứ hai: 60km / (v1 + 20km/h) = t2Ta có 2 phương trình:
t1 + t2 + 0.5 = 8 (giờ) (với thời gian nghỉ là 30 phút)v1 * t1 + (v1 + 20km/h) * t2 = 120kmTa có thể giải hệ phương trình bằng cách sử dụng phương pháp thế, bằng cách giải một biến trong hai phương trình trên và thay vào phương trình còn lại.
Vận tốc dự định của ô tô là: v1 = 80 km/h.

Lời giải:
Giả sử vận tốc xe máy là $a$ km/h thì vận tốc ô tô là $a+15$ km/h
Xe máy xuất phát trước ô tô 30 phút mà đến sau ô tô 15 phút, tức là thời gian xe máy đi quãng đường HN-TH dài hơn ô tô 45 phút, hay $\frac{3}{4}$ h
Ta có:
Thời gian xe máy đi là: $\frac{135}{a}$ (h)
Thời gian ô tô đi: $\frac{135}{a+15}$ (h)
Theo bài ra: $\frac{135}{a}-\frac{135}{a+15}=\frac{3}{4}$
$\Leftrightarrow a(a+15)=2700$
$\Leftrightarrow (a-45)(a+60)=0$
Vì $a>0$ nên $a=45$ (km/h) -- đây chính là vận tốc xe máy
Vận tốc ô tô là: $45+15=60$ (km/h)

Gọi quãng đường từ Hà Nội - Thanh Hóa là : x
Thời gian đi nửa quãng đường : \(\frac{x}{2.40}\)
Thời gian đi nữa quảng đường còn lại: \(\frac{x}{2.\left(40+20\right)}\)
Thời gian đi về \(:\frac{x}{50}\)
Tổng thời gian đi là: 9h2p - 2h30p = 6h32 p \(=\frac{98}{15}h\)
Ta có phương trình:
\(\frac{a}{2.40}+\frac{a}{2.\left(40+20\right)}+\frac{a}{50}=\frac{98}{15}\)
\(\Leftrightarrow a=160\)
Vậy quãng đường Hà Nội-Thanh Hóa daì 160km