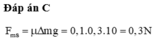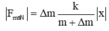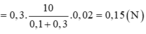Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Một vật rơi từ độ cao h xuống đĩa thì vận tốc lúc chạm đĩa tại O của vật cũng chính là vận tốc lớn nhất của con lắc dao động thỏa mãn:
\(v_{max}^2 - v_0^2 = 2gh\)
=> \(v_{max} = \sqrt{2gh} = \sqrt{2.10.1} = \sqrt{20} (m/s)\)
Mà: \(v_{max} = A \omega=> A = \frac{v_{max}}{\omega} = \frac{\sqrt{20}}{10} \approx0,447m.\)
Lực kéo lớn nhất tác dụng lên điểm I chính là lực đàn hồi lớn nhất khi lò xo dãn.nhiều nhất.(ở vị trí biên A)
\(F_ {maxI} = kA = 10.0,447 = 4,47N.\)
Chọn đáp án.B.

+ Giai đoạn 1: Vật rơi xuống đĩa, vận tốc của vật khi chạm đĩa: \(v=\sqrt{2gh}=\sqrt{2.10.0,5}=\sqrt{10}\)(m/s) = \(100\sqrt{10}\)(cm/s)
Với h = 50 cm là độ cao so với mặt đĩa
+ Giai đoạn 2: Vật và đĩa cùng dao động, là dao động điều hòa.
Ở VTCB, lò xo nén: \(\Delta l_0=\frac{mg}{k}=\frac{0,1.10}{80}=0,0125m=1,25cm\)
Điều đó có nghĩa, sau khi vật chạm mặt đĩa thì nó đang có li độ -1,25cm và vận tốc \(100\sqrt{10}\)(cm/s)
\(\omega=\sqrt{\frac{k}{m}}=\sqrt{\frac{80}{0,1}}=20\sqrt{2}\)(rad/s)
Biên độ dao động: \(A=\sqrt{x^2+\frac{v^2}{\omega^2}}=\sqrt{1,25^2+\left(\frac{100\sqrt{10}}{20\sqrt{2}}\right)^2}=11,25cm\)
Lực nén của lò xo lên sàn đạt cực đại khi vật ở vị trí thấp nhất (biên độ dương)
Khi đó, lò xo nén: 11,25 + 1,25 = 12,5cm = 0,125m.
Lực đàn hồi max: \(F_{đh}=80.0,125=10N\)

Đáp án C
Cường độ âm do các loa truyền đến điểm M :
I M = ( I N + I N ' ) ≡ P 2 π 1 a 2 + b 2 4 + 1 a 2 + b 2 4 + h 2
Để IM là lớn nhất thì biểu thức dưới mẫu phải nhỏ nhất. Ta có :
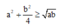 dấu bằng xảy ra khi
a
=
b
2
⇒
a
=
3
b
=
6
dấu bằng xảy ra khi
a
=
b
2
⇒
a
=
3
b
=
6
Giá trị cường độ âm khi đó
( I M ) m a x = 5 P m a x 108 π = 10
⇒ P m a x = 678 W

- Nên nhớ các công thức trong dao động tắt dần:
- Quãng đường vật đi được đến khi dừng hẳn:
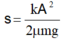
Thay số vào ta được:
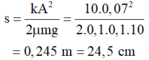

Đáp án B
Nên nhớ các công thức trong dao động tắt dần:
Quãng đường vật đi được đến khi dừng hẳn: s = k A 2 2 μ m g
Thay số vào ta được: s = 10 . 0 , 07 2 2 . 0 , 1 . 0 , 1 . 10 = 0 , 245 m = 24 , 5 c m