Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

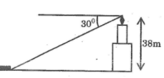
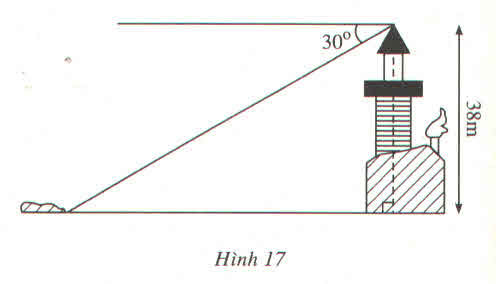
Khoảng cách từ đảo đến chân cột đèn biển là cạnh kề với góc 30 ° , chiều cao của cột đèn biển là cạnh đối diện với góc 30 °
Vậy khoảng cách từ đảo đến chân đèn là:
38.cotg 30 ° ≈ 65,818 (cm)

*gọi: A là đỉnh ngọn đèn biển; B là chân đèn; C là hòn đảo
>>tam giác ABC vuông tại B có: AB=38m; góc ACB=30 độ
>>khoảng cách từ đảo đến chân đèn:
AC=AB/tan30=38/tan30=38căn3=65,8179m

Khoảng cách từ đảo đến chân đèn là:
\(38\cdot\cot30^0\simeq65,818\left(cm\right)\)

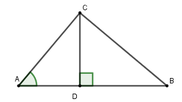
Độ cao của máy bay là CD, độ dài AB = 100m. Đào đứng ở A, Mai đứng ở B
Gọi AD = x (0 < x < 100) => BD = 150 – x
Xét ACD vuông tại D, ta có CD = AD.cot A = x . c o t 45 0 = x
Xét ABD vuông tại D, ta có CD = BD.cot B = (150 – x). c o t 35 0
Nên x = (150 – x). c o t 35 0 => x ≈ 88,22 (thỏa mãn)
=> CD = x = 88,22m
Vậy độ cao của diều lúc đó so với mặt đất là 88,22m
Đáp án cần chọn là: D

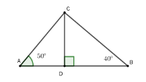
Độ cao của diều là CD, độ dài AB = 100m. Trung đứng ở A, Dũng đứng ở B
Gọi AD = x (0 < x < 100)
=> BD = 100 – x
Xét ACD vuông tại D, ta có CD = AD.tan A = x . tan 50 0
Xét ABD vuông tại D, ta có CD = BD.tan B = (100 – x). tan 40 0
Nên x . tan 50 0 = (100 – x). tan 40 0
![]()
Vậy độ cao của diều lúc đó so với mặt đất là 49,24m
Đáp án cần chọn là: B
Đề bài sai rồi em (hoặc là thiếu dữ liệu)
Không thể tính được khoảng cách giữa 2 hòn đảo chỉ với các số liệu này.
A B x z D C
Giả sử người đó đứng ở vị trí A, hòn đảo thứ nhất ở vị trí B với \(\widehat{BAx}=40^0\) và \(AB=115\) nên điểm B cố định
Khi đó, nếu ta dựng tia Az sao cho \(\widehat{xAz}=60^0\) thì hòn đảo thứ 2 nằm ở 1 vị trí bất kì trên tia Az đều thỏa mãn bài toán
Nghĩa là khoảng cách giữa 2 hòn đảo thay đổi và không thể tính được. Em có thể đặt hòn đảo thứ 2 ở C hay D hay 1 điểm nào đó tùy thích. Rõ ràng là các đoạn BC và BD khác nhau về độ dài nhưng đều thỏa mãn yêu cầu bài toán.