Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gắn hệ trục Oxy vào chiếc cổng, gọi chiều cao của cổng là h ta vẽ lại parabol như dưới đây:
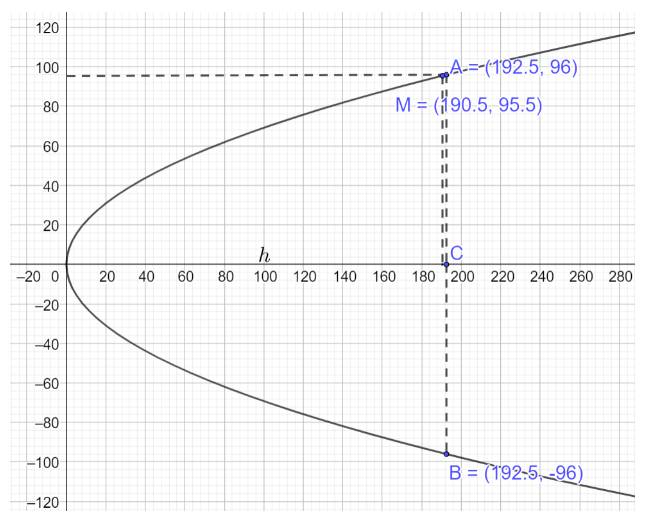
Phương trình parabol mô phỏng cổng có dạng \({y^2} = 2px\)
Theo giả thiết \(AB = 2{y_A} = 192 \Rightarrow {y_A} = 96,OC = h \Rightarrow M\left( {h - 2;95,5} \right),A\left( {h;96} \right)\)
Thay tọa độ các điểm \(M\left( {h - 2;95,5} \right),A\left( {h;96} \right)\) vào phương trình \({y^2} = 2px\) ta có:
\(\left\{ \begin{array}{l}95,{5^2} = 2p\left( {h - 2} \right)\\{96^2} = 2ph\end{array} \right. \Rightarrow \left\{ \begin{array}{l}p = \frac{{383}}{{16}}\\h \simeq 192,5\end{array} \right.\)
Vậy chiều cao của cổng gần bằng 192,5 m

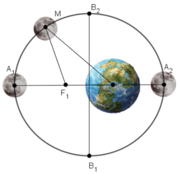
Theo đề bài có:
Độ dài trục lớn của elip bằng 769266km ⇒ A1A2 = 2a = 769266 ⇒ a = 384633
Độ dài trục nhỏ của elip bằng 768106km ⇒ B1B2 = 2b = 768106 ⇒ b = 384053
⇒ c2 = a2 – b2 = 445837880 ⇒ c ≈ 21115
⇒ F1F2 = 2c = 42230
⇒ A1F1 = A2F2 = (A1A2 – F1F2)/2 = 363518
+ Trái Đất gần Mặt Trăng nhất khi Mặt Trăng ở điểm A2
⇒ khoảng cách ngắn nhất giữa Trái Đất và Mặt Trăng bằng A2F2 = 363518 km
+ Trái Đất xa Mặt Trăng nhất khi Mặt Trăng ở điểm A1
⇒ khoảng cách xa nhất giữa Trái Đất và Mặt Trăng bằng:
A1F2 = A1F1 + F1F2 = 405748 km.

Tam giác ABC vuông tại B nên ta có: \(\tan C = \frac{{AB}}{{CB}} \Leftrightarrow AB = \tan {32^ \circ }.(1 + x)\)
Tam giác ADB vuông tại B nên ta có: \(\tan D = \frac{{AB}}{{DB}} \Leftrightarrow AB = \tan {40^ \circ }.x\)
\(\begin{array}{l} \Rightarrow \tan {32^ \circ }.(1 + x) = \tan {40^ \circ }.x\\ \Leftrightarrow x.(\tan {40^ \circ } - \tan {32^ \circ }) = \tan {32^ \circ }\\ \Leftrightarrow x = \frac{{\tan {{32}^ \circ }}}{{\tan {{40}^ \circ } - \tan {{32}^ \circ }}}\\ \Leftrightarrow x \approx 2,9\;(km)\end{array}\)
\( \Rightarrow AB \approx \tan {40^ \circ }.2,92 \approx 2,45\;(km)\)
Vậy chiều cao của ngọn núi là 2,45 km.

a) Chọn hệ trục tọa độ Oxy với gốc tọa độ tại tâm đáy nhà vòm, trục tung thẳng đứng

Nhà vòm có dạng elip nên có phương trình chính tắc là \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) (với a,b>0)
Ta có chiều cao 8 m nên \(OA = b = 8\), chiều rộng của vòm là 20 m, suy ra \(BC = 2a = 20 \Rightarrow a = 10\).
Suy ra, phương trình miêu tả hình dáng nhà vòm là \(\frac{{{x^2}}}{{100}} + \frac{{{y^2}}}{{64}} = 1\)
b) Điểm đó cách chân tưởng 5 m tương ứng cách tâm 5 m (vì từ tâm vòm đến tưởng là 10 m)
Thay \(x = 5\) vào phương trình \(\frac{{{x^2}}}{{100}} + \frac{{{y^2}}}{{64}} = 1\), ta tìm được \(y = 4\sqrt 3 \)
Vậy khoảng cách phương thẳng đứng từ một điểm cách chân tường 5 m đến nóc nhà vòm là \(4\sqrt 3\) m
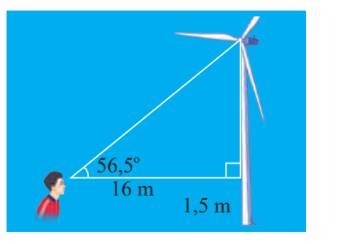






Cách 1:
Ta có: \(\widehat B = {90^o} - 56,{5^o} = 33,{5^o}\)
Áp dụng định lí sin, ta có: \(\frac{{BC}}{{\sin A}} = \frac{{AC}}{{\sin B}}\)
\( \Rightarrow BC = \sin A.\frac{{AC}}{{\sin B}} = \sin 56,{5^o}.\frac{{16}}{{\sin 33,{5^o}}} \approx 24,2\;(m)\)
Vậy khoảng cách từ tâm của cánh quạt đến mặt đất là \(24,2 + 1,5 = 25,7(m)\)
Cách 2:
\(\tan A = \frac{{BC}}{{AC}} \Rightarrow BC = AC.\tan A = 16.\tan 56,{5^o} \approx 24,2\)
Vậy khoảng cách từ tâm của cánh quạt đến mặt đất là \(24,2 + 1,5 = 25,7(m)\)