Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi khoảng cách từ tâm đối xứng đến đáy tháp là z
Suy ra khoảng cách từ tâm đối xứng đến nóc tháp là \(\frac{2}{3}z\)
Ta có \(z + \frac{2}{3}z = 150 \Rightarrow z = 90\)
Thay \(y = 90\) vào phương trình \(\frac{{{x^2}}}{{{{28}^2}}} - \frac{{{y^2}}}{{{{42}^2}}} = 1\) ta tìm được \(x = 4\sqrt {274} \)
Thay \(y = 60\) vào phương trình \(\frac{{{x^2}}}{{{{28}^2}}} - \frac{{{y^2}}}{{{{42}^2}}} = 1\) ta tìm được \(x = 4\sqrt {149} \)
Vậy bán kính đường tròn nóc và bán kính đường tròn đáy của tháp lần lượt là \(4\sqrt {149} \) m và \(4\sqrt {274} \)m

Gọi khoảng cách từ tâm đối xứng đến đỉnh tháp là z
Suy ra khoảng cách từ tâm đối xứng đến đáy tháp là 2z
Ta có \(z + 2z = 120 \Rightarrow z = 40\)
Thay \(y = 40\) vào phương trình \(\frac{{{x^2}}}{{{{27}^2}}} - \frac{{{y^2}}}{{{{40}^2}}} = 1\) ta tìm được \(x = 27\sqrt 2 \)
Thay \(y = 80\) vào phương trình \(\frac{{{x^2}}}{{{{27}^2}}} - \frac{{{y^2}}}{{{{40}^2}}} = 1\) ta tìm được \(x = 27\sqrt 5 \)
Vậy bán kính đường tròn nóc và bán kính đường tròn đáy của tháp lần lượt là \(27\sqrt 2 \) và \(27\sqrt 5 \)

a: A(1;2); B(2;1)
=>\(\overrightarrow{AB}=\left(1;-1\right)\)
=>VTPT là (1;1)
Phương trình đường thẳng AB là:
1(x-1)+2(y-1)=0
=>x-1+2y-2=0
=>x+2y-3=0
b:
M(1;3); Δ: 3x+4y+10=0
Khoảng cách từ M đến Δ là:
\(d\left(M;\text{Δ}\right)=\dfrac{\left|1\cdot3+3\cdot4+10\right|}{\sqrt{3^2+4^2}}=\dfrac{\left|3+12+10\right|}{5}=5\)

75 cm trên bản vẽ ứng với 2,5 đơn vị trên mặt phẳng tọa độ.
Gọi M là điểm trên vòm ô thoáng, có hoành độ 2,5 và tung độ là h.
M thuộc elip nên \(\frac{{2,{5^2}}}{{16}} + \frac{{{h^2}}}{4} = 1\)
\(\Leftrightarrow h = \sqrt {4.\left( {1 - \frac{{2,{5^2}}}{{16}}} \right)} = \frac{{\sqrt {39} }}{4} \approx 1,56\)
Vậy độ cao h trên thực tế là: \(h = 1,56.30 = 46,8\) cm

a) (E): 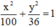 có a = 10; b = 6 ⇒ c2 = a2 – b2 = 64 ⇒ c = 8.
có a = 10; b = 6 ⇒ c2 = a2 – b2 = 64 ⇒ c = 8.
+ Tọa độ các đỉnh của elip là: A1(-10; 0); A2(10; 0); B1(0; -6); B2(0; 6)
+ Tọa độ hai tiêu điểm của elip: F1(-8; 0) và F2(8; 0)
+ Vẽ elip:
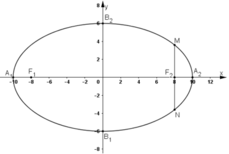
b) Ta có: M ∈ (E) ⇒ MF1 + MF2 = 2a = 20 (1)
MN // Oy ⇒ MN ⊥ F1F2 ⇒ MF12 – MF22 = F1F22 = (2c)2 = 162
⇒ (MF1 + MF2).(MF1 – MF2) = 162
⇒ MF1 – MF2 = 12,8 (Vì MF1 + MF2 = 20) (2).
Từ (1) và (2) ta có hệ phương trình
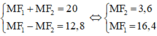
Vậy MN = 2.MF2 = 7,2.

Ta có: Chiều cao và chiều rộng của đường hầm là 4m, 10m nên ta có: \(a = 5,b = 4\)
Nên phương trình chính tắc của elip có dạng \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{{16}} = 1\)
Nhập phương trình elip theo cú pháp x^2/25 + y^2/16 = 1 {y>=0} vào vùng nhập lệnh ta có hình vẽ mô phỏng đường hầm dưới đây
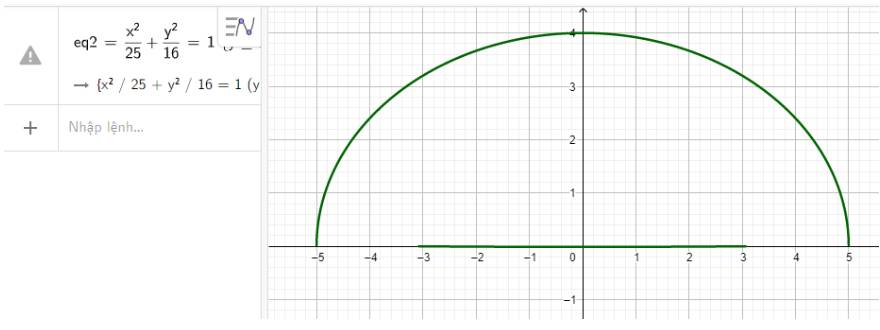
Vậy phương trình mô phỏng đường hầm là \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{{16}} = 1\) với \(y \ge 0\)
Và có hình mô phỏng thực tế như hình trên




a) Chọn hệ trục tọa độ Oxy với gốc tọa độ tại tâm đáy nhà vòm, trục tung thẳng đứng
Nhà vòm có dạng elip nên có phương trình chính tắc là \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) (với a,b>0)
Ta có chiều cao 8 m nên \(OA = b = 8\), chiều rộng của vòm là 20 m, suy ra \(BC = 2a = 20 \Rightarrow a = 10\).
Suy ra, phương trình miêu tả hình dáng nhà vòm là \(\frac{{{x^2}}}{{100}} + \frac{{{y^2}}}{{64}} = 1\)
b) Điểm đó cách chân tưởng 5 m tương ứng cách tâm 5 m (vì từ tâm vòm đến tưởng là 10 m)
Thay \(x = 5\) vào phương trình \(\frac{{{x^2}}}{{100}} + \frac{{{y^2}}}{{64}} = 1\), ta tìm được \(y = 4\sqrt 3 \)
Vậy khoảng cách phương thẳng đứng từ một điểm cách chân tường 5 m đến nóc nhà vòm là \(4\sqrt 3\) m