Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đổi 1 giờ 20 phút = 80 phút
Vì vận tốc tỉ lệ nghịch với thời gian, người đi xe đạp có vận tốc bằng 2 lần vận tốc người đi bộ thì thời gian người đi xe đạp đi quãng đường AB chỉ bằng một nửa thời gian người đi bộ đi trên cùng một quãng đường đó.
Người đi xe đạp đi quãng đường AB hết:
80:2=40(phút)

độ dài quãng đường AB là
5,6 x 1 = 5,6 km
vận tốc xe đạp là
5,6 x 2 = 11,2 km/giờ
thời gian đi xe đạp hết quãng đường AB là
5,6 : 11,2 = 0,5 giờ = 30 phút
đs......

đổi 20 phút = 1/3 giờ
độ dài quãng đường AB là
4,2 x 1/3 = 1,4 km
vận tốc xe đạp là
4,2 x 2 = 8,4 km/h
thời gian đi hết quãng đường AB bằng xe đạp là
1,4 : 84 = 1/6 giờ = 10phút

Nếu người đó đi xe đạp với tốc độ gấp hai lần thì khoảng thời gian đi hết quãng đường đó sẽ giảm đi hai lần.
Thời gian người đó đi hết quãng đường AB là:
\(20\div2=10\)(phút)

Đổi : 40 phút = \(\frac{2}{3}\)giờ
Quãng đường AB dài là :
\(5,8 \times\frac{2}{3}=\frac{58}{15} \)( km )
Vận tốc của người đó khi đi xe đạp là :
\( 5,8 \times 2 = 11,6 \)( km/h )
Người đó đi hết quãng đường AB bằng xe đạp hết số thời gian là :
\(\frac{58}{15}\div11,6=\frac{1}{3}\) ( giờ )
Đáp số : \(\frac{1}{3}\) giờ
#zinc

t=2h30p=2,5h
độ dài quãng đg là: s=2,5.42=105 km
khi ng đó đi vs vận tốc =5/2 vận tốc ban đầu thì tốn: 105:(5/2.42)=1h
vậy mất 1 giờ

Tóm tắt
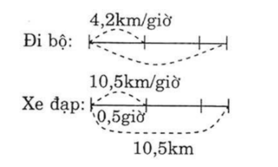
2 giờ 30 phút = 2,5 giờ
Quãng đường AB là:
4,2 ⨯ 2,5 = 10,5 (km)
Vận tốc người đi xe đạp là:
4,2 × 5/2 = 10,5 (km/giờ)
Thời gian người đi xe đạp đi hết quãng đường AB:
10,5 : 10,5 = 1 (giờ)
Đáp số: 1 giờ
Ta có : \(S=t\times v\)
Trong đó : S là quãng đường đi (km)
t là thời gian đi (km/h)
v là vận tốc đi của người đó (h)
Gọi S là độ dài quãng đường AB
Đổi : \(40phut=\dfrac{2}{3}gio\)
Từ công thức ở trên ta có :
\(S=\dfrac{2}{3}\times5,5\)
Nếu người đó đi xe đạp thì vận tốc bằng 2 lần vận tốc đi bộ nên vận tốc người đó đi xe đạp là :
\(5,5\times2=11\left(km/h\right)\)
Do cùng đi trên một quãng đường AB nên nếu vận tốc tăng lên thì thời gian phải giảm đi nên ta có thể lập thành một bài tìm x đơn giản như :
\(S=t\times11\)
Trong đó : t là thời gian cần tìm .
mà : \(S=\dfrac{2}{3}\times5,5\)
\(\Rightarrow S=\dfrac{t}{2}\times5,5\times2\)
\(\Rightarrow t=\dfrac{1}{3}gio\)
\(Vậy...\)