Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D.
Phương pháp:
Giả sử anh A nợ ngân hàng M ngàn đồng), mỗi tháng anh A gửi vào ngân hàng a ngàn đồng, lãi suất ngân hàng là r (%). Số tiền anh A còn nợ ngân hàng :

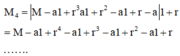

Gọi n là số tháng (tính từ năm thứ hai) mà sinh viên A trả được hết nợ, ta có:
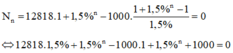
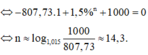
Vậy, số tháng để sinh viên A trả hết nợ là: 12 + 15 = 27 (tháng)

Đáp án B
Phương pháp:
Sử dụng bài toán: Hàng tháng, một người vay (gửi) ngân hàng số tiền là a đồng với lãi suất hàng tháng là r thì sau n tháng người ấy có tổng số tiền nợ (gửi) ngân hàng là
![]()
Tính số tiền anh sinh viên nợ sau 2 năm
Tính số tiền anh sinh viên trả được sau 22 tháng
Tính số tiền nợ còn lại.
Cách giải:
Trong thời gian từ tháng 01/09/2014 đến hết tháng 08/2016 là 24 tháng thì mỗi tháng anh sinh viên vay ngân hàng 3 triệu với lãi suất 0,8%/tháng nên số tiền anh nợ ngân hàng tất cả là:
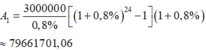
đồng
Trong thời gian từ tháng 09/2016 đến cuối tháng 06/2018 là 22 tháng thì mỗi tháng anh sinh viên trả ngân hàng 2 triệu với lãi suất 0,8%/ tháng nên số tiền anh trả được ngân hàng là:
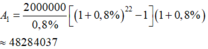
đồng
Tính đến tháng 06/2018 thì số tiền nợ ngân hàng của anh là
![]()
Số tiền anh còn nợ là
![]()


Đến năm thứ 16 thì người đó được tăng lương số lần là: 16 3 = 5 lần.
Áp dụng công thức: S n = A 1 + r n ta có số tiền người đó nhận được ở tháng đầu tiên của năm thứ 16 là:
6 ( 1 + 10 % ) 5 = 6 . 1 . 1 5 triệu đồng

Câu 2:
\(=0.168\cdot4=\dfrac{84}{125}=67,2\%\)
Câu 7:
Số học sinh nữ là:
40x2/5=16(bạn)
Câu 10:
\(=\left(\dfrac{1}{4}\cdot\dfrac{9}{2}+\dfrac{1}{2}\cdot50\right)\cdot\left(\dfrac{3}{20}-\dfrac{3}{4}\cdot\dfrac{1}{5}\right)=0\)
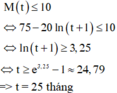
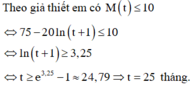
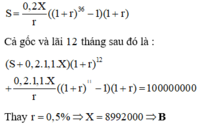



Theo công thức tính tỉ lệ % đã cho thì cần tìm
nghiệm t của bất phương trình;
75 - 20 ln 1 + t ≤ 10 ⇔ ln 1 + t ≥ 3 , 25 ⇒ t ≥ 24 , 79
Vậy sau khoảng 25 tháng (tức 2 năm 1 tháng) thì học
sinh nhớ được danh sách đó là dưới 10%
Đáp án C