Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)
Sắp xếp:
5,5 7,4 10,2 11,0 11,4 12,2 12,5 13,1 13,4 13,8
n=10
Số trung bình: \(\overline X = 11,05\)
Trung vị: 11,8
Khoảng biến thiên: R=13,8-5,5=8,3

Độ lệch chuẩn: 8,1
b) Làm trò các số liệu trong mẫu:
Giá trị | Làm tròn | Sai số |
5,5 | 6 | 0,5 |
7,4 | 7 | 0,4 |
10,2 | 10 | 0,2 |
11,0 | 11 | 0 |
11,4 | 11 | 0,4 |
12,2 | 12 | 0,2 |
12,5 | 13 | 0,5 |
13,1 | 13 | 0,1 |
13,4 | 13 | 0,4 |
13,8 | 14 | 0,2 |
Sai số tuyệt đối của các phép làm tròn không vượt quá 0,5.

Tham khảo:
a)
Bước 1: Ta có:
| Loại A | Loại B |
Giá mua vào | 10 triệu đồng/1 máy | 20 triệu đồng/1 máy |
Lợi nhuận | 2,5 triệu đồng/1 máy | 4 triệu đồng/1 máy |
Bước 2: Lập hệ bất phương trình
Vì số lượng máy là số tự nhiên nên ta có \(x \ge 0;y \ge 0\)
Vốn nhập vào x máy loại A và y máy loại B là \(10x + 20y\)(triệu đồng)
4 tỉ đồng=4000 (triệu đồng)
Vì số vốn ban đầu không vượt quá 4 tỉ đồng nên ta có bất phương trình
\(10x + 20y \le 4000\) \( \Leftrightarrow x + 2y \le 400\)
Vì tổng nhu cầu hàng tháng sẽ không vượt quá 250 máy nên ta có \(x + y \le 250\).
Vậy ta có hệ bất phương trình \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x + 2y \le 400\\x + y \le 250\end{array} \right.\)
Bước 3: Xác định miền nghiệm
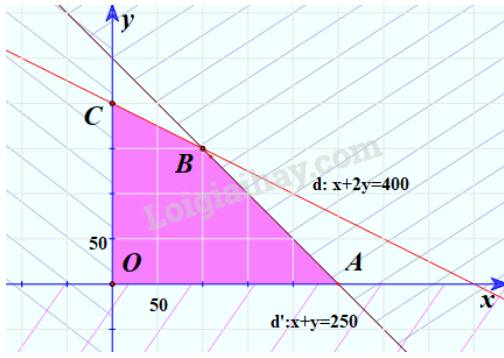
Miền nghiệm là tứ giác OABC với tọa độ các đỉnh này là O(0;0), A(250;0), B(100;150), C(0;200)
b) Lợi nhuận hàng tháng là F(x;y)=2,5x+4y(triệu đồng)
c) Ta cần tìm giá trị lớn nhất của F(x;y) khi (x;y) thỏa mãn hệ bất phương trình \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x + 2y \le 400\\x + y \le 250\end{array} \right.\)
Ta có F(0;0)=0, F(250;0)=2,5.250+4.0=625
F(100;150)=2,5.100+4.150=850
F(0;200)=2,5.0+4.200=800
Giá trị lớn nhất là F(100;150)=850.
Vậy cửa hàng cần đầu tư kinh doanh 100 máy A và 150 máy B.
a) Số máy tính loại A cửa hàng cần nhập trong một tháng là x (máy), số máy tính loại B cửa hàng cần nhập trong một tháng là y (máy) (x,y≥0).
Do tổng nhu cầu hàng tháng sẽ không vượt quá 250 máy: x + y ≤ 250
Tổng số vốn cửa hàng cần nhập hai loại A và B: 10x + 20y (triệu đồng)
Vì mỗi chiếc máy tính loại A có giá 10 triệu và mỗi máy tính loại B có giá 20 triệu nên tổng số vốn cửa hàng cần nhập hai loại A và B: 10x + 20y (triệu đồng)
Vì số vốn ban đầu không vượt quá 4 tỉ đồng nên ta có: 10x + 20y ≤ 4 000 hay x + 2y ≤ 400.
Ta có hệ bất phương trình: \(\left\{{}\begin{matrix}x\ge0\\y\ge0\\x+y\le250\\x+2y\le400\end{matrix}\right.\)
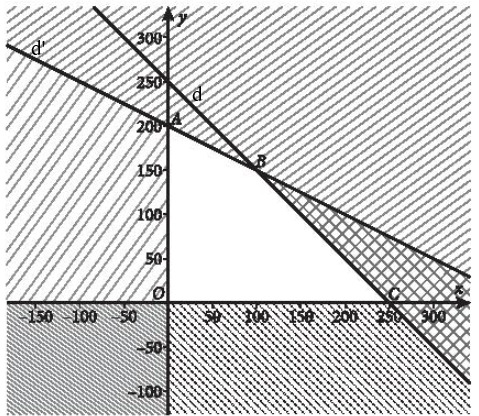
Ta xác định miền nghiệm của hệ bất phương trình trên:
+) Miền nghiệm D1 của bất phương trình x ≥ 0 là nửa mặt phẳng bờ Oy chứa điểm (1;0).
+) Miền nghiệm D2 của bất phương trình y ≥ 0 là nửa mặt phẳng bờ Ox chứa điểm (0;1).
+) Xác định miền nghiệm D3 của bất phương trình x + y ≤ 250.
- Vẽ đường thẳng d: x + y = 250.
- Vì 0 + 0 = 0 < 250 nên tọa độ điểm O(0;0) thỏa mãn bất phương trình x + y ≤ 250
Do đó miền nghiệm D3 của bất phương trình x + y ≤ 250 là nửa mặt phẳng bờ d chứa gốc tọa độ.
+) Xác định miền nghiệm D4 của bất phương trình x + 2y ≤ 400.
- Vẽ đường thẳng d’: x + 2y = 400.
- Vì 0 + 2.0 = 0 < 400 nên tọa độ điểm O(0;0) thỏa mãn bất phương trình x + 2y < 400
Do đó miền nghiệm D4 của bất phương trình x + 2y < 400 là nửa mặt phẳng bờ d’ chứa gốc tọa độ.
Miền nghiệm của hệ bất phương trình trên là tứ giác OABC với O(0;0), A(0; 200), C(100;150), B(250;0)
b) Lợi nhuận mà cửa hàng thu được trong tháng đó khi bán x máy tính loại A và y máy tính loại B là: F(x;y) = 2,5x + 4y (triệu đồng).
Vậy F(x;y) = 2,5x + 4y.
c) Bài toán chuyển về tìm giá trị lớn nhất của F(x;y) với (x;y) thuộc miền nghiệm của hệ bất phương trình \(\left\{{}\begin{matrix}x\ge0\\y\ge0\\x+y\le250\\x+2y\le400\end{matrix}\right.\)
Người ta đã chứng minh được, giá trị F(x; y) lớn nhất tại (x; y) là tọa độ của một trong bốn đỉnh O; A; B; C.
Tại O(0; 0), ta có: F(0; 0) = 2,5 . 0 + 4 . 0 = 0;
Tại A(0; 200), ta có: F(0; 200) = 2,5 . 0 + 4 . 200 = 800;
Tại B(100; 150), ta có: F(100; 150) = 2,5 . 100 + 4 . 150 = 850;
Tại B(250; 0), ta có: F(250; 0) = 2,5 . 250 + 4 . 0 = 625.
Do đó F(x;y) lớn nhất bằng 850 tại x = 100 và y = 150.
Vậy cửa hàng cần nhập 100 máy loại A, 150 máy loại B để cửa hàng thu được lợi nhuận lớn nhất là 850 triệu đồng.

a. Số trung bình:
(5,5 + 7,4 +10,2 + 11,0 + 11,4 + 12,2 + 12,5 + 13,1 +13,4 +13,8) : 10 = 11,05
Trung vị: 11,8
Khoảng biến thiên: R=13,8-5,5=8,3
|
Giá trị |
Độ lệch |
Bình phương độ lệch |
|
5,5 |
5,55 |
30,8025 |
|
7,4 |
3,65 |
13,3225 |
|
10,2 |
0,85 |
0,7225 |
|
11,0 |
0,05 |
0,0025 |
|
11,4 |
-0,35 |
0,1225 |
|
12,2 |
-1,15 |
1,3225 |
|
12,5 |
-1,45 |
2,1025 |
|
13,1 |
-2,05 |
4,2025 |
|
13,4 |
-2,35 |
5,5225 |
|
13,8 |
-2,75 |
7,5625 |
|
Tổng |
65,6850 |
|
Độ lệch chuẩn: 8,1
b) Làm trò các số liệu trong mẫu:
|
Giá trị |
Làm tròn |
Sai số |
|
5,5 |
6 |
0,5 |
|
7,4 |
7 |
0,4 |
|
10,2 |
10 |
0,2 |
|
11,0 |
11 |
0 |
|
11,4 |
11 |
0,4 |
|
12,2 |
12 |
0,2 |
|
12,5 |
13 |
0,5 |
|
13,1 |
13 |
0,1 |
|
13,4 |
13 |
0,4 |
|
13,8 |
14 |
0,2 |
Sai số tuyệt đối của các phép làm tròn không vượt quá 0,5.
Tham khảo trên mạng nhé
a. Số trung bình:
(5,5 + 7,4 +10,2 + 11,0 + 11,4 + 12,2 + 12,5 + 13,1 +13,4 +13,8) : 10 = 11,05
Trung vị: 11,8
Khoảng biến thiên: R=13,8-5,5=8,3
|
Giá trị |
Độ lệch |
Bình phương độ lệch |
|
5,5 |
5,55 |
30,8025 |
|
7,4 |
3,65 |
13,3225 |
|
10,2 |
0,85 |
0,7225 |
|
11,0 |
0,05 |
0,0025 |
|
11,4 |
-0,35 |
0,1225 |
|
12,2 |
-1,15 |
1,3225 |
|
12,5 |
-1,45 |
2,1025 |
|
13,1 |
-2,05 |
4,2025 |
|
13,4 |
-2,35 |
5,5225 |
|
13,8 |
-2,75 |
7,5625 |
|
Tổng |
65,6850 |
|
Độ lệch chuẩn: 8,1
b) Làm trò các số liệu trong mẫu:
|
Giá trị |
Làm tròn |
Sai số |
|
5,5 |
6 |
0,5 |
|
7,4 |
7 |
0,4 |
|
10,2 |
10 |
0,2 |
|
11,0 |
11 |
0 |
|
11,4 |
11 |
0,4 |
|
12,2 |
12 |
0,2 |
|
12,5 |
13 |
0,5 |
|
13,1 |
13 |
0,1 |
|
13,4 |
13 |
0,4 |
|
13,8 |
14 |
0,2 |
Sai số tuyệt đối của các phép làm tròn không vượt quá 0,5.
Gọi số dinh dưỡng A cần là x và số dinh dưỡng B cần là y
Ta có hệ điều kiện: \(\left\{{}\begin{matrix}4\le x+y\le10\\0\le x\le6\\0\le y\le5\\\dfrac{x}{2}\le y\le3x\end{matrix}\right.\) (1)
Hàm chi phí: \(f\left(x;y\right)=8x+7y\)
Phần đồ thị biểu diễn miền hệ điều kiện (1) là phần đa giác ABCDEF như bên dưới:
Trong đó \(A\left(\dfrac{5}{3};5\right)\) ; \(B\left(5,5\right)\) ; \(C\left(6;4\right)\) ; \(D\left(6;3\right)\) ; \(E\left(\dfrac{8}{3};\dfrac{4}{3}\right)\) ; \(F\left(1;3\right)\)
Thay tọa độ của 6 điểm trên vào hàm \(f\left(x;y\right)\) và tính giá trị, ta thấy \(f\left(x;y\right)\) nhỏ nhất tại \(F\left(1;3\right)\) tức cần 1 dinh dưỡng A và 3 dinh dưỡng B để chi phí nhỏ nhất
tóm tắt sương sương
1 ngày x-A
y-B Nên 8x+7y min
\(\left\{{}\begin{matrix}4\le x+y\le10\\0\le x\le6\\0\le y\le5\\\dfrac{1}{2}x\le y\le3x\end{matrix}\right.\)
nhìn đề hơi loại ạ