Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: sin β = 10/300 = 1/30
Suy ra: β ≈ 1 ° 55 '
Vậy khi máy bay bắt đầu hạ cánh thì góc nghiêng là 1 ° 55 '

a.
Nếu phi công muốn tạo góc nghiêng 5 độ so với mặt đất thì phải cách sân bay:
$\frac{8}{\sin 5^0}=91$ (km)
b.
Nếu cách sân bay 280 km máy bay bắt đầu hạ cạnh thì góc nghiêng là $\alpha$ thỏa mãn: $\frac{8}{\sin \alpha}=280$
$\sin \alpha= \frac{8}{280}=\frac{1}{35}$
$\Rightarrow \alpha = 1,64^0$

Độ cao của máy bay là cạnh góc vuông đối diện với góc 3 ° , khoảng cách từ máy bay đến sân bay là cạnh huyền
Vậy khoảng cách từ máy bay đến sân bay là:



Độ cao của máy bay là CD, độ dài AB = 60m; D A C ^ = 30 0 ; D B C ^ = 50 0
Gọi BC = x => AC = 60 + x
Xét tam giác BDC vuông tại C có:
![]()
Xét tam giác ADC vuông tại C có:
![]()
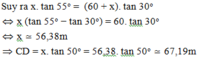
Vậy độ cao của máy bay so với mặt đất là 67,19m
Đáp án cần chọn là: C
Cảm ơn các bạn! Mình làm được rồi nhé!