Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Vận tốc 240 km/h nên \(\left| {\overrightarrow v } \right| = AC = 240\)
Áp dụng các tính chất trong tam giác vuông ta có
\(AB = DC = AC.\cos (\widehat {CAB}) = 240.\cos (30^\circ ) = 120{\sqrt 3 }\)
\(AD = BC = AC.\sin (\widehat {CAB}) = 240.\sin (30^\circ ) = 120\)
b) Xem A là gốc tọa độ nên ta có \(\overrightarrow {AB} = 120\overrightarrow i ,\overrightarrow {AD} = 120{\sqrt 3 }\overrightarrow j ,\overrightarrow v = \overrightarrow {AC} = 120\overrightarrow i + 120{\sqrt 3 }\overrightarrow j \)
c)
Ta có \(\overrightarrow v = 120\overrightarrow i + 120{\sqrt 3 }\overrightarrow j \)
Vậy tọa độ của vectơ \(\overrightarrow v \) là \(\left( {120;120{\sqrt 3 }} \right)\)

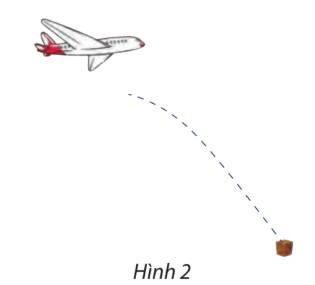
Gắn hệ trục tọa độ Oxy như hình dưới:

Gọi A vị trí hàng rơi xuống, khi đó \({y_A} = 0\). Ta có, tọa độ của A thỏa mãn:
\(\left\{ \begin{array}{l}x = 50t\\y = 80 - \frac{1}{2}.9,8.{t^2}\end{array} \right.\)
Mà \({y_A} = 0 \Rightarrow 0 = 80 - \frac{1}{2}.9,8.{t^2} \Leftrightarrow {t^2} \approx 16,33 \Rightarrow t \approx 4(s)\)
Do đó \({x_A} = 50.4 = 200(m)\) hay khoảng cách giữa máy bay và thùng hàng cứu trợ là 200m.
Vậy để thùng hàng cứu trợ rơi đúng vị trí được chọn thì máy bay cần thả hàng khi cách điểm đó 200m.

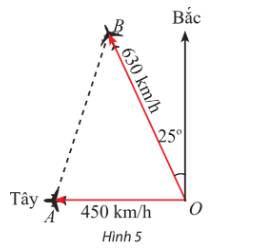
Ta có: \(\widehat {BOA} = {90^o} - {25^o} = {65^o}.\)
Sau 90 phút = 1,5 giờ:
Máy bay thứ nhất đi được quãng đường (OA) là: \(450.1,5 = 675\;(km)\)
Máy bay thứ hai đi được quãng đường (OB) là: \(630.1,5 = 945\;(km)\)
Áp dụng định lí cosin trong tam giác OAB, ta có:
\(\begin{array}{l}A{B^2} = O{A^2} + O{B^2} - 2OA.OB\cos O\\ \Leftrightarrow A{B^2} = {675^2} + {945^2} - 2.675.945\cos {65^o}\\ \Rightarrow AB \approx 900\end{array}\)
Vậy sau 90 phút, hai máy bay cách nhau khoảng 900 km.

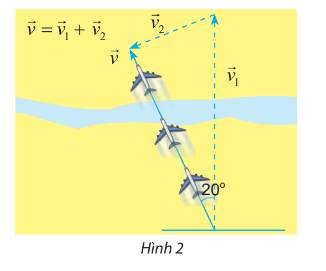
Từ giả thiết ta có:
+) Vectơ tương ứng với vận tốc máy bay là vectơ \(\overrightarrow {{v_1}} \)
+) Vectơ tương ứng với vận tốc máy bay so với mặt đất là vectơ \(\overrightarrow v \)
+) Vectơ tương ứng với vận tốc gió là vectơ \(\overrightarrow {{v_2}} \)
Ta có : \(\left| {\overrightarrow {{v_1}} } \right| = 45;\left| {\overrightarrow v } \right| = 38;\left( {\overrightarrow {{v_1}} ,\overrightarrow v } \right) = 20^\circ \)
Áp dụng định lý cosin ta có:
\(\left| {\overrightarrow {{v_2}} } \right| = \sqrt {{{\left| {\overrightarrow v } \right|}^2} + {{\left| {\overrightarrow {{v_1}} } \right|}^2} - 2\left| {\overrightarrow v } \right|.\left| {\overrightarrow {{v_1}} } \right|.\cos \left( {\overrightarrow v ,\overrightarrow {{v_1}} } \right)} \)
\( = \sqrt {{{38}^2} + {{45}^2} - 2.38.45.\cos 20^\circ } \simeq 16\) (m/s)
Vậy tốc độ của gió gần bằng 16 m/s

a) Đường thẳng \(\Delta \) có vectơ chỉ phương \(\overrightarrow v = \left( {3; - 4} \right)\),nên có vectơ pháp tuyền là \(\overrightarrow n = \left( {4;3} \right)\) và đi qua \(A(1;2)\)
Ta có phương trình tổng quát là
\(4(x - 1) + 3(y - 2) = 0 \Leftrightarrow 4x + 3y - 10 = 0\)
b) Điểm M thuộc trục hoành nên tung độ bằng 0
Thay \(y = 0\) vào phương trình \(4x + 3y - 10 = 0\) ta tìm được \(x = \frac{5}{2}\)
Vậy \(\Delta \) cắt trục hoành tại điểm \(M\left( {\frac{5}{2};0} \right)\)

a) Vị trí máy bay vào lúc 14 giờ 30 phút là: \(\left\{ \begin{array}{l}x = \frac{{1600}}{3} - \frac{{1400}}{3}.\frac{1}{2} = 300\\y = \frac{{1900}}{3} - \frac{{1400}}{3}.\frac{1}{2} = 400\end{array} \right.\)
Vậy tọa độ máy bay là \(\left( {300;400} \right)\). Thời điểm này máy bay đã xuất hiện trên màn hình ra đa.
b) Ta có: \(MO = \sqrt {{{\left( {\frac{{1600}}{3} - \frac{{1400}}{3}t} \right)}^2} + {{\left( {\frac{{1900}}{3} - \frac{{1400}}{3}t} \right)}^2}} \).
Do có \(M{O_{\min }} = 50\sqrt 2 \Leftrightarrow t = \frac{5}{4}\).
Vậy sau khi bay \(\frac{5}{4} = 1,25\) (giờ) tức là lúc 15h15p thì máy bay gần ra đa nhất và khoảng cách từ ra đa đến máy bay khi đó là \(50\sqrt 2 \left( {km} \right)\).
c) Máy bay rời khỏi màn hình ra đa khi mà khoảng cách từ M đến O lớn hơn 500km tức là:
\(MO = \sqrt {{{\left( {\frac{{1600}}{3} - \frac{{1400}}{3}t} \right)}^2} + {{\left( {\frac{{1900}}{3} - \frac{{1400}}{3}t} \right)}^2}} \ge 500 \Leftrightarrow \left[ \begin{array}{l}t = \frac{1}{2}\\t = 2\end{array} \right.\)
Vậy sau khi bay được 2h tức là lúc 16h thì máy bay thoát khỏi màn hình ra đa.

Đoạn thẳng AB có hướng được gọi là vecto \(\overrightarrow {AB} \).

a) Chọn hệ trục tọa độ Oxy với gốc tọa độ tại tâm đáy nhà vòm, trục tung thẳng đứng

Nhà vòm có dạng elip nên có phương trình chính tắc là \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) (với a,b>0)
Ta có chiều cao 8 m nên \(OA = b = 8\), chiều rộng của vòm là 20 m, suy ra \(BC = 2a = 20 \Rightarrow a = 10\).
Suy ra, phương trình miêu tả hình dáng nhà vòm là \(\frac{{{x^2}}}{{100}} + \frac{{{y^2}}}{{64}} = 1\)
b) Điểm đó cách chân tưởng 5 m tương ứng cách tâm 5 m (vì từ tâm vòm đến tưởng là 10 m)
Thay \(x = 5\) vào phương trình \(\frac{{{x^2}}}{{100}} + \frac{{{y^2}}}{{64}} = 1\), ta tìm được \(y = 4\sqrt 3 \)
Vậy khoảng cách phương thẳng đứng từ một điểm cách chân tường 5 m đến nóc nhà vòm là \(4\sqrt 3\) m




Để xác định tọa độ của máy bay ta phải lập phương trình quỹ đạo bay của máy bay hay chính là lập phương trình đường thẳng.