Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Theo phương trình hóa học, ta thấy nếu đốt cháy hết 1 mol phân tử khí CH4 thì phải cần 2 mol phân tử khí O2. Do đó thể tích khí oxi cần dùng để đốt cháy hoàn toàn 2 lít khí metan là:
VO2 = 2 . 2 = 4 lít.
b) Theo phương trình phản ứng, khi đốt cháy hoàn toàn 0,15 mol khí metan thì cũng sinh ra 0,15 mol khí cacbon đioxit. Do đó thể tích khí CO2 thu được là:
VCO2 = 0,15 . 22,4 = 3,36 lít.
c) Tỉ khối của khí metan và không khí là:
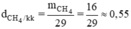
Vậy khí metan nhẹ hơn không khí 0,55.

a) CH4 + 2O2 --to--> CO2 + 2H2O
b) \(V_{O_2}=\dfrac{56}{5}=11,2\left(l\right)\)
=> \(n_{O_2}=\dfrac{11,2}{22,4}=0,5\left(mol\right)\)
PTHH: CH4 + 2O2 --to--> CO2 + 2H2O
_____0,25<--0,5-------->0,25
=> VCH4 = 0,25.22,4 = 5,6 (l)
c)
mCO2 = 0,25.44 = 11 (g)

1. Trong 1000 m 3 khí thiên nhiên có 850 m 3 C H 4
2 C H 4 → 1500 ° C C 2 H 2 + 3 H 2
CH ≡ CH + HCl → 150 - 200 ° C , H g C l 2 C H 2 = C H - C l
Khối lượng vinyl clorua thu được (nếu hiệu suất các quá trình là 100%) là:
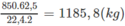
Với hiệu suất cho ở đầu bài, khối lượng vinyl clorua là:
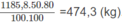
2. Nhiệt lượng cần dùng để làm nóng 100 lít nước từ 20 ° C lên 100 ° C :
100.4,18.(100 - 20) = 33440 (kJ)
Vì 20% nhiệt lượng đã toả ra môi trường nên nhiệt lượng mà khí thiên nhiên cần cung cấp phải là :
Đặt số mol C 2 H 6 tà x thì số mol C H 4 là 85. 10 - 1 x.
Ta có 1560x + 88085. 10 - 1 x = 41800
x = 462. 10 - 2
Thể tích khí thiên nhiên cần dùng:
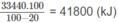

n CH4 = 1.85% = 0,85(mol)
n C2H6 = 1.10% = 0,1(mol)
$CH_4 + 2O_2 \xrightarrow{t^o} CO_2 + 2H_2O$
$C_2H_6 + \dfrac{7}{2} O_2 \xrightarrow{t^o} 2CO_2 + 3H_2O$
Theo PTHH :
n O2 = 2n CH4 + 7/2 n C2H6 = 2,05(mol)
n không khí = n O2 : 20% = 2,05 : 20% = 10,25(mol)

a)
CH4 + 2O2 --to--> CO2 + 2H2O
2C2H6 + 7O2 --to--> 4CO2 + 6H2O
b) \(n_{CH_4}=\dfrac{85\%.112}{22,4}=4,25\left(mol\right)\)
\(n_{C_2H_6}=\dfrac{112.10\%}{22,4}=0,5\left(mol\right)\)
=> \(Q=4,25.880+0,5.1560=4520\left(kJ\right)\)
c) \(Q=2000.4,18.\left(100-20\right)=668800\left(J\right)=668,8\left(kJ\right)\)
Giả sử có a mol khí thiên nhiên
=> \(\left\{{}\begin{matrix}n_{CH_4}=a.85\%=0,85a\left(mol\right)\\n_{C_2H_6}=a.10\%=0,1a\left(mol\right)\end{matrix}\right.\)
\(Q=880.0,85a+1560.0,1a=668,8\left(kJ\right)\)
=> a = \(\dfrac{418}{565}\left(mol\right)\) => \(V=\dfrac{418}{565}.22,4=16,572\left(l\right)\)