Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Gọi R,h lần lượt là bán kính đáy và chiều cao của khối trụ ⇒ h = 6 R = 6 . Thể tích của khối trụ là V = πR 2 h = π . 1 2 . 6 = 6 π . Khối cầu bên trong khối trụ có bán kính là R = 1 ⇒ V C = 4 3 π . R 3 = 4 3 π . Khối nón bên trong khối trụ có bán kính đáy là R = 1 và chiều cao h - 2R = 4. Suy ra thể tích khối nón là V N = 1 3 πR 2 h = 1 3 . π . 1 2 . 4 = 4 3 π . Do đó, thể tích lượng nước còn lại bên trong khối trụ là V 0 = V - V C + V N = 6 π - 2 . 4 π 3 = 10 π 3 . Vậy tỉ số cần tính là T = V 0 V = 10 π 3 : 6 π = 5 9 .

Đáp án A
Phương pháp:
Sử dụng công thức tính thể tích khối trụ V = π r 2 h
Cách giải:
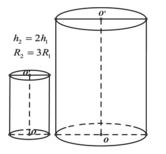
Từ công thức V = π r 2 h ta có: Thể tích khối trụ tăng lên 2.3 2 = 18 lần.

Chọn C.
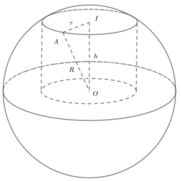
Phương pháp: Dựa vào dữ kiện bài toán lập hàm số và tìm giá trị lớn nhất, nhỏ nhất.

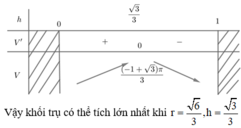

Đáp án D
Lời giải:

Lập bảng biến thiên ta thấy h0 là điểm cực đại của hàm số f(h) và f(h0) là GTLN của f(h) trên (0;2R)
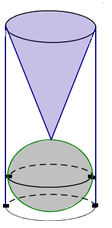
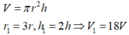

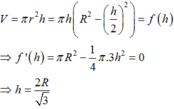
Đáp án B.
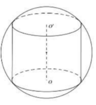
Gọi h là chiều cao của khối trụ, r là bán kính
h 2 + h 2 = 2 R 2 ⇒ h 2 = 2 R 2 ⇒ h = R 2
⇒ r = 1 2 h = R 2 2
⇒ V t r u = B . h = πr 2 h = π R 2 2 . R 2 = πR 3 2 2