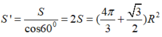Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Phương pháp:
+) Chứng minh mặt phẳng (P) không cắt đáy (O';R)
+) Tìm phần hình chiếu của mặt phẳng (P) trên mặt đáy. Tính S h c
+) Sử dụng công thức S h c = S . cos 60
Cách giải:
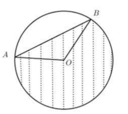
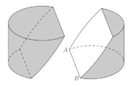
Gọi M là trung điểm của AB ta có:
O M = O A 2 − A B 2 2 = R 2 − 3 R 2 4 = R 2
Giả sử mặt phẳng (P) cắt trục OO’ tại I. Ta có : IA = IB nên Δ I A B cân tại I, do đó M I ⊥ A B


Vậy diện tích phần thiết diện cần tìm là :
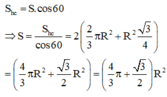

Đáp án A
Khoảng cách từ tâm đến đáy mặt phẳng cắt là 3 => Chiều rộng của hình chữ nhật là a = 2 R 2 - d 2 = 2 . 5 2 - 3 2 = 8
Vậy diện tích S của thiết diện là S = 8.7 = 56.

Đáp án A
Khoảng cách từ tâm đáy đến mặt phẳng cắt là 3
Suy ra chiều rộng của hình chữ nhật là
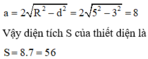

Đáp án D
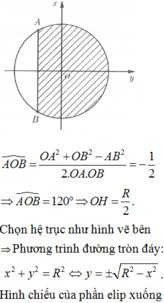
cos A O B ^ = O A 2 + O B 2 - A B 2 2 . O A . O B = - 1 2 ⇒ A O B ^ = 120 0 ⇒ O H = R 2
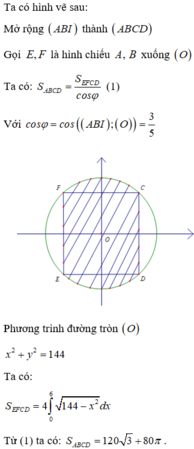
Chọn hệ trục tọa độ như hình vẽ pt đường tròn đáy là:
x 2 + y 2 = R 2 ⇔ y = ± R 2 - x 2
Hình chiếu của phần elip xuống đáy là miền gạch chéo như hình vẽ
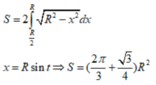
Gọi diện tích phần elip cần tính là S’. theo công thức hình chiếu ta có
S ' = S cos 60 0 = 2 S = ( 4 π 3 + 3 2 ) R 2

Đáp án D
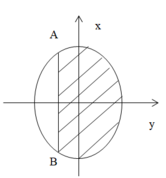
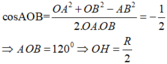
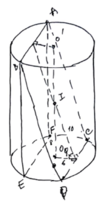
Chọn hệ trục tọa độ như hình vẽ => pt đường tròn đáy là:
![]()
Hình chiếu của phần elip xuống đáy là miền gạch chéo như hình vẽ
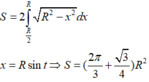
Gọi diện tích phần elip cần tính là S’. theo công thức hình chiếu ta có