Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1.Thời gian hòn đá chạm đất là:
\(t=\sqrt{\dfrac{2h}{g}}=\sqrt{\dfrac{2\cdot500}{9.8}}=10.1\left(s\right)\)
2. Quảng đường vật đi được trong 5s
\(s=\dfrac{1}{2}gt^2=\dfrac{1}{2}\cdot9,8\cdot5^2=122,5\left(m\right)\)

Độ cao nơi thả hòn đá: \(h=\dfrac{1}{2}gt^2m\)
Quãng đường hòn đá rơi trước khi chạm đất 1s: \(h'=\dfrac{1}{2}g\left(t-1\right)^2m\)
Quãng đường hòn đá rơi trong giây cuối cùng: \(\Delta h=h-h'\)
\(\Leftrightarrow34,3=\dfrac{1}{2}gt^2-\dfrac{1}{2}g\left(t-1\right)^2\)
\(\Leftrightarrow34,3=\dfrac{1}{2}9,8t^2-\dfrac{1}{2}9,8\left(t-1\right)^2\)
\(\Rightarrow t=4s\)
Vậy:.................

Nếu gọi s là quãng đường viên đá đi được sau khoảng thời gian t kể từ khi bắt đầu rơi tới khi chạm đất và gọi s 1 là quãng đường viên đá đi được trước khi chạm đất 1 s, tức là sau khoảng thời gian t 1 = t -1 thì ta có các công thức
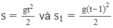
Từ đó suy ra quãng đường viên đá đi được trong 1 s cuối trước khi chạm đất là:
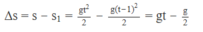
Với ∆ s = 24,5 m và g = 10 m/ s 2 , ta tìm được khoảng thời gian rơi tự do của viên đá
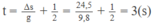

a) Độ sâu của giếng: \(h=\dfrac{1}{2}gt^2=\dfrac{1}{2}\cdot10\cdot3^2=45m\)
Vận tốc hòn đá khi chạm đấy giếng: \(v=g\cdot t=10\cdot3=30\)m/s
b) Quãng đường hòn đá rơi trong giây thứ ba:
\(S=\dfrac{1}{2}gt^2-\dfrac{1}{2}g\left(t-1\right)^2=\dfrac{1}{2}\cdot10\cdot3^2-\dfrac{1}{2}\cdot10\cdot2^2=25m\)
c) Thời gian hòn đá rơi 20m cuối cùng trước khi chạm giếng:
\(t=\sqrt{\dfrac{2\cdot S}{g}}=\sqrt{\dfrac{2\cdot20}{10}}=2\left(s\right)\)

Đáp án:
+Thời gian rơi
+Vận tốc chạm đất
+Quãng đường rơi trong giây cuối cùng khi chạm đất:


Quãng đường vật rơi trong 1s cuối cùng:
∆ h = h - h 7 = 75 m
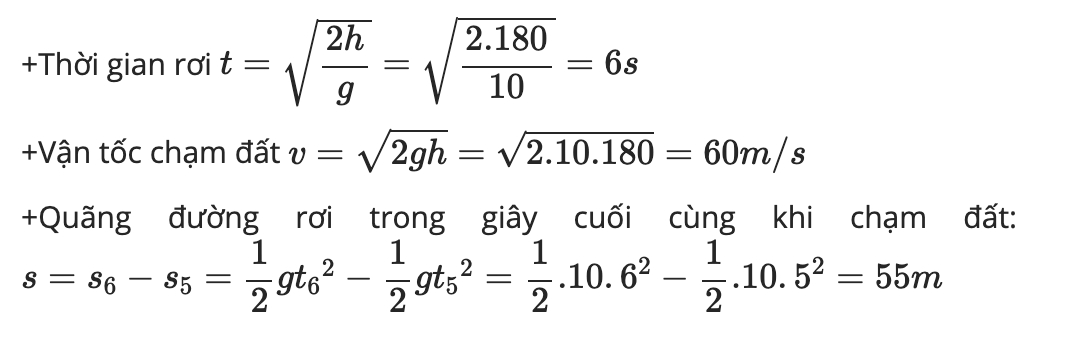
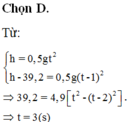
Tóm tắt: \(S=24,5m;t=1s;g=9,8\)m/s2
\(t=?\)
Bài giải:
Thời gian hòn đá rơi đến khi chạm đất:
\(S=\dfrac{1}{2}gt^2\Rightarrow t=\sqrt{\dfrac{2S}{g}}=\sqrt{\dfrac{2\cdot24,5}{9,8}}=\sqrt{5}\approx2,24s\)