Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Vì cả 3 lần đo đều cho 1 kết quả nên L ¯ = 2,345 m
Sai số ngẫu nhiên DL = 0
+ Sai số của thiết bị là DL’ = 1 mm = 0,001 m
® L = (2,345 ± 0,001) m.

- Vì cả 3 lần đo đều cho 1 kết quả nên
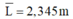
- Sai số ngẫu nhiên ΔL = 0
- Sai số của thiết bị là ΔL’ = 1 mm = 0,001 m
⇒ L = (2,345 ± 0,001) m.

+ 10 dao động toàn phần và tính được kết quả t = 20 , 102 ± 0 , 269 s ⇒ T = 2 , 0102 ± 0 , 0269 s
T = 2 π l g ⇒ g = 4 π 2 l T 2 ⇒ g ¯ = 4 π 2 l ¯ T ¯ 2 = 4 π 2 .1 , 000 2 , 0102 2 ≈ 9 , 899 m/s 2
Δ g g ¯ = Δ l l ¯ + 2 Δ T T ¯ = 0 , 001 1 + 2. 0 , 0269 2 , 0102 ≈ 0 , 0277635 ⇒ Δ g = 9 , 899.0 , 0277635 ≈ 0 , 275 m/s 2
Gia tốc trọng trường do học sinh đo được tại nới làm thí nghiệm là g = 9 , 899 ± 0 , 275 m/s 2 .
Chọn đáp án C

Chọn C.
10 dao động toàn phần và tính được kết quả
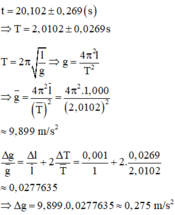
Gia tốc trọng trường do học sinh đo được tại nới làm thí nghiệm là 9 , 899 ± 0 , 275 m / s 2 .

Phương pháp: Sử dụng công thức tính chu kì dao động của con lắc đơn và công thức tính sai số trong thực hành thí nghiệm
Cách giải:
Công thức xác định độ lớn gia tốc trọng trường:
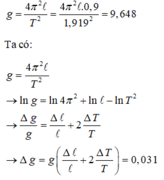
Đáp án A

Đáp án A
Phương pháp: Sử dụng công thức tính chu kì con lắc đơn T= 2 π l g kết hợp với lí thuyết sai số trong thí nghiệm thực hành
Cách giải:
Chu kì của con lắc đơn: T= 2 π l g
Gia tốc rơi tự do được xác định theo công thức:
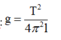
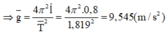
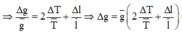
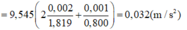
Do đó: g = 9,545 ± 0,032 m/s => Chọn A

Đáp án A
Phương pháp: Sử dụng công thức tính chu kì dao động của con lắc đơn và công thức tính sai số trong thực hành thí nghiệm
Cách giải :
Công thức xác định độ lớn gia tốc trọng trường:
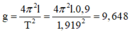
Ta có:
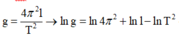
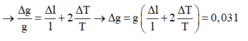

+ Ta có T = 2 π l g → g ¯ = 2 π 2 l ¯ T 2 ¯ = 9 , 64833 m / s 2
→ Sai số tuyệt đối của phép đo: Δ g = g ¯ Δ l l ¯ + 2 Δ T T ¯ = 0 , 0314 m / s 2
Ghi kết quả: T = 9 , 648 ± 0 , 031 m / s 2
Đáp án B
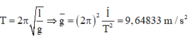
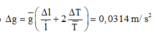
Chọn đáp án C
Vì cả 3 lần đo đều cho 1 kết quả nên L- = 2,345 m
Sai số ngẫu nhiên DL = 0
Sai số của thiết bị là DL’ = 1 mm = 0,001 m
® L = (2,345 ± 0,001) m