Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B.
Phương pháp: Coi đáy của hình trụ là mặt phẳng cắt mặt cầu. Áp dụng công thức

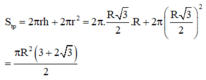

Theo công thức ta có:
Sxq = 2πrh = 2√3 πr2
Stp = 2πrh + 2πr2 = 2√3 πr2 + 2 πr2 = 2(√3 + 1)πr2 ( đơn vị thể tích)
b) Vtrụ = πR2h = √3 π r3
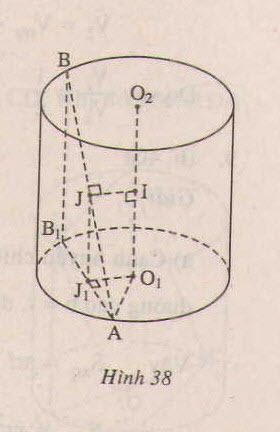
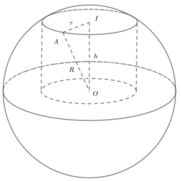
c) Giả sử trục của hình trụ là O1O2 và A nằm trên đường tròn tâm O1, B nằm trên đường tròn tâm O2; I là trung điểm của O1O2, J là trung điểm cảu AB. Khi đó IJ là đường vuông góc chung của O1O2 và AB. Hạ BB1 vuông góc với đáy, J1 là hình chiếu vuông góc của J xuống đáy.
Ta có là trung điểm của
,
= IJ.
Theo giả thiết = 300.
do vậy: AB1 = BB1.tan 300 = = r.
Xét tam giác vuông
AB1 = BB1.tan 300 = O1J1A vuông tại J1, ta có: =
-
.
Vậy khoảng cách giữa AB và O1O2 :

Đáp án A
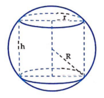
Gọi bán kính đáy và chiều cao của hình trụ lần lượt là r và h. Khi đó thiết diện qua trục của hình trụ là một hình chữ nhật có kích thước hai cạnh là 2r và h. Diện tích hình chữ nhật đó là S = 2 r h .
Quan sát hình vẽ, ta thấy R 2 = h 2 2 + r 2 ⇔ h = 2 R 2 − r 2 = 2 3 a 2 − r 2 .
Khi đó S = 2 r h = 4 r 3 a 2 − r 2 ≤ 4. r 2 + 3 a 2 − r 2 2 2 = 6 a 2 . Dấu “=” xảy ra khi và chỉ khi
r = 3 a 2 − r 2 ⇔ 2 r 2 = 3 a 2 ⇔ r = a 6 2 ⇒ h = 2 3 a 2 − 3 a 2 2 = a 6
Vậy diện tích toàn phần của hình trụ (T) là
S t p = 2 π r h + 2 π r 2 = 2 π a 6 . a 6 2 + 2 π a 6 2 2 = 9 π a 2 (đvdt).

Chọn D.
Phương pháp:
Gọi M;N lần lượt là hình chiếu của A,B trên đáy còn lại không chứa A,B.
Từ đó ta sử dụng định lý Pytago để tìm cạnh của hình vuông
Sử dụng công thức: Diện tích hình vuông cạnh x bằng x2 .
Cách giải:
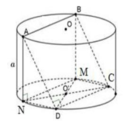
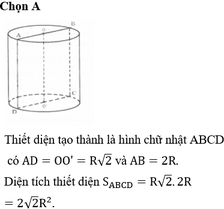
Xét hình trụ như trên. Gọi cạnh hình vuông ABCD là x ( x > 0)
Gọi M;N lần lượt là hình chiếu của A,B trên đáy còn lại không chứa A,B.
Vì AB / /DC; AB = DC => AB / /MN / /DC; AB = MN = DC hay MNDC là
hình bình hành tâm O’.
Lại có MD = NC = 2a nên MNDC là hình chữ nhật.
Suy ra


Chọn C.
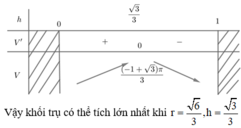
Phương pháp: Dựa vào dữ kiện bài toán lập hàm số và tìm giá trị lớn nhất, nhỏ nhất.


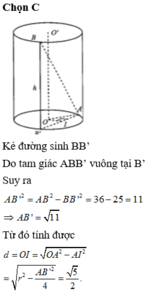
Đáp án B
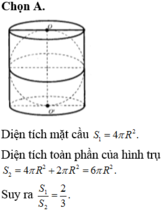
Gọi h, r lần lượt là chiều cao và bán kính đường tròn đáy của hình trụ.
Khi đó, bán kính mặt cầu ngoại tiếp hình trụ là R 2 = r 2 + h 2 4
Theo bài ra, ta có h = R nên suy ra R 2 = r 2 + h 2 4 ⇔ r 2 = 3 R 2 4 ⇔ r = R 3 2
Diện tích toàn phần hình trụ là:
S t p = 2 πr 2 + 2 πrh = 2 πr r + h = 2 π . R 3 2 . R 3 2 + R = 3 + 2 3 πR 2 2 .