Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- So sánh được diện tích hình tam giác AMN bằng 1 2 diện tích hình tam giác ABN (Cùng đường cao từ B, cạnh đáy bằng nửa)
- So sánh được diện tích hình tam giác ABN bằng 1 2 diện tích hình tam giác ABC
- Kết luận diện tích hình tam giác AMN bằng 1 4 diện tích hình tam giác ABC

a,(bạn vẽ hình ra đi) Tam giác AMN và ABN đều có đỉnh chung và đáy bằng nhau=)Hai tam giác bằng nhau
b, Tam giác AMN và ABC đều cùng đỉnh nhưng tam giác ABC có đáy gấp đôi tam giác AMN=)Tam giác ABC có diện tích gấp đôi tam giác AMN
Cho mk 1 k nhaaaaa

Nối C với M
Tam giác ACM và tam giác ACB có chung đường cao hạ từ C xuống cạnh AB; đáy AM = 1/2 đáy AB (Vì M là điểm chính giữac cạnh AB)
=> S (ACM) = 1/2 S(ABC) = 1/2 x 160 = 80 cm2
Xét tam giác AMN và tam giác ACM có chung chiều cao hạ từ M xuống cạnh AC; đáy AN = 1/4 đáy AC
=> S (AMN) = 1/4 x S (ACM) = 1/4 x 80 = 20 cm2

a: Xét ΔABC có \(AN=\dfrac{1}{2}AC\)
nên \(S_{ABN}=\dfrac{1}{2}\cdot S_{ABC}=\dfrac{1}{2}\cdot45=22,5\left(cm^2\right)\)
Xét ΔABN có \(AM=\dfrac{1}{2}AB\)
nên \(S_{AMN}=\dfrac{1}{2}\cdot S_{ABN}=\dfrac{1}{2}\cdot22,5=11,25\left(cm^2\right)\)
b: Xét ΔABC có
M,N lần lượt là trung điểm của AB,AC
=>MN là đường trung bình của ΔABC
=>MN//BC và \(MN=\dfrac{BC}{2}\)
Xét ΔABK có MI//BK
nên \(\dfrac{MI}{BK}=\dfrac{AI}{AK}\left(1\right)\)
Xét ΔACK có IN//KC
nên \(\dfrac{IN}{KC}=\dfrac{AI}{AK}\left(2\right)\)
Từ (1),(2) suy ra \(\dfrac{MI}{BK}=\dfrac{IN}{KC}\)
mà MI=IN(I là trung điểm của MN)
nên BK=KC
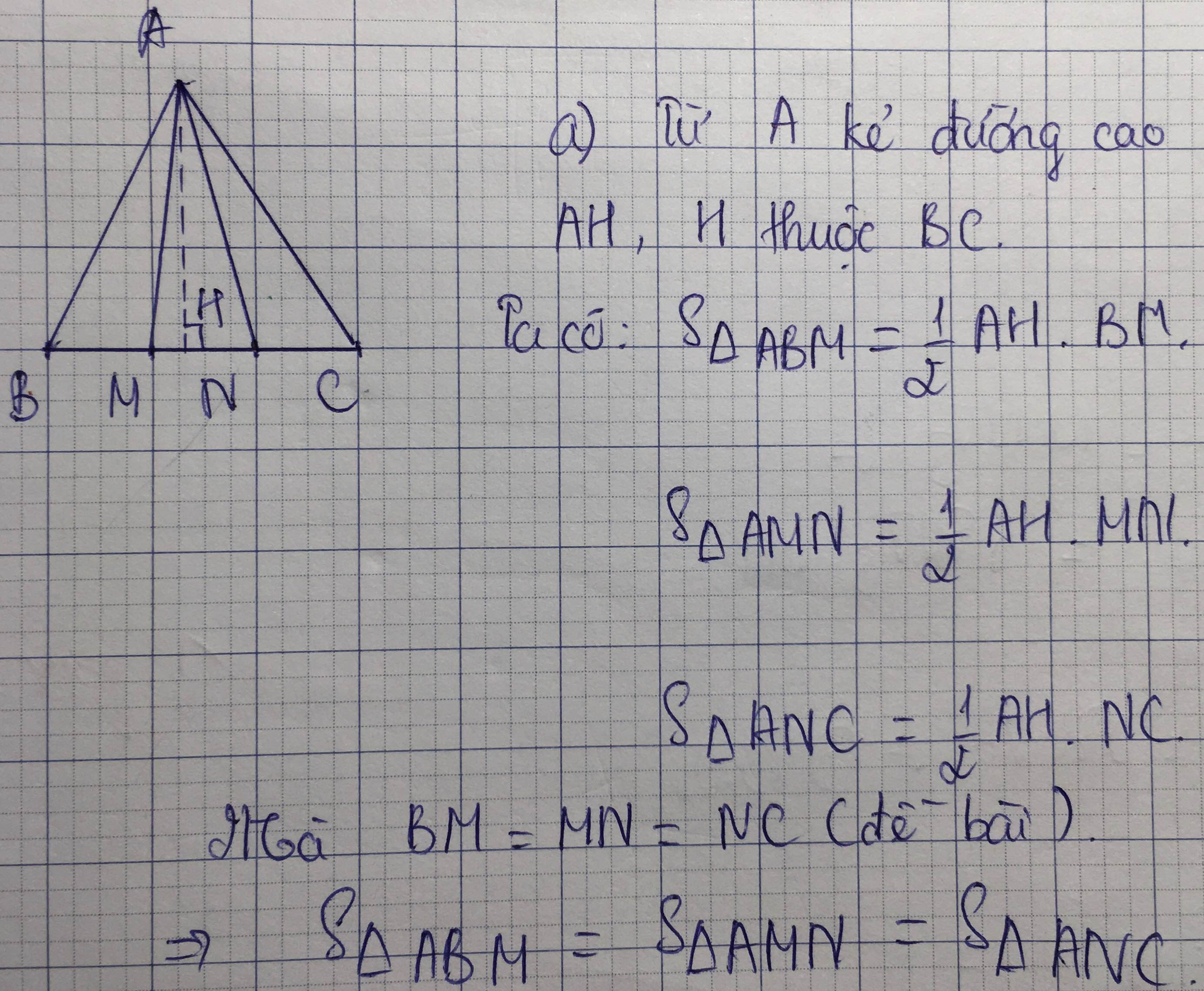

Hẳn bài giải ra cơ