Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án là C
l0=50cm
m=400g
k=50N/m
Khi thả rơi. Lực trọng trường là P=mg= 4N
=>độ dãn của lò xo là Dl0=P/K=4/50=8cm
Khi lò xo dãn 14cm độ trung bình theo chiều dài của lò xo là 14/50=0,28
Khi lò xo bị giữ chặt ở vị trí cách điểm treo 32 cm => độ dài phần lò xo dãn tự do là 50+14-32=32cm
Trong đó chiều dài phần lò xo tự do khi không bị dãn là 32-32.0,28=23,04cm
=>vị trí cân bằng mới cách vị trí lò xo bị giữ là: 23,04-Dl0=31,04 cm
=> Khoảng cách từ vị trí cân bằng mới tới điểm treo của lò xo là 32+31,04=63,04cm
Khoảng cách lớn nhất từ điểm treo tới vật m sau đó có thể đạt là 63,04+A, với A là biên độ dao động.
63,04+A>63,04
Nên Khoảng cách lớn nhất từ điểm treo tới vật m sau đó có thể đạt được phải lớn hơn 63,04cm
Trong các đáp án, chỉ có Đáp án C 66,8cm thỏa mãn.
Vậy chọn C là đáp án đúng

Đáp án D
Vậ n tốc của vật m’ ngay khi va chạm: m'gh = 1 2 m v 0 2 ⇒ v 0 = 2 g h = 4 m / s
Vị trí cân bằng mới của hệ hai vật lệch xuống dưới một đoạn: ∆ l 0 = m g k = 100 . 10 - 3 . 10 20 = 5 c m
Vận tốc của hai vật sau va chạm : V = m ' v 0 m + m ' = v 0 2 = 2 m / s
Biên độ dao động của vật: A = ∆ l 0 2 + V ω 2 = 5 17 cm
Vật m’ sẽ tách khỏi vật m tại vị trí lò xo không biến dạng, khi đó ta có thời gian tương ứng là
t = 1 ω a r sin ∆ 0 A + T 2 ≈ 0 , 389 s

Giải thích: Đáp án D
Phương pháp:
Sử dụng công thức vật rơi tự do
Định luật bảo toàn động lượng
Hệ thức độc lập theo thời gian của x và v
Cách giải:
Vận tốc của m’ ngay trước khi rơi vào m là ![]()
Vận tốc của hai vật ngay sau va chạm: 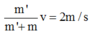 (do sau va chạm hai vật chuyển động với cùng vận tốc)
(do sau va chạm hai vật chuyển động với cùng vận tốc)
Vị trí cân bằng của cả hai vật cách vị trí va chạm một đoạn: 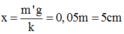
Sau va chạm cả hai cùng đi xuống đến vị trí có tọa độ: 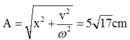
Phân tích các lực tác dụng lên m’ có: phản lực
N
⇀
, lực quán tính ![]() và trọng lực P’ = m’g
và trọng lực P’ = m’g
Thời điểm t vật m’ rời lần thứ nhất thì N = 0; 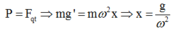
Với 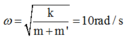
Ta có: x = 0,1m = 10 cm. (Tọa độ x được tính so với gốc tọa độ O là VTCB khi m’ chưa khỏi rời m, và chiều dương trục Ox chọn hướng theo phương thẳng đứng lên trên).
Chu kì dao động: 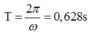
Dùng vòng tròn lượng giác ta tìm được: 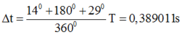

Đáp án D
+ Tại thời điểm ban đầu ta có ∆ l 0 = 10 c m
+ Đưa vật tới vị trí lò xo giãn 20 cm thì có thêm vật m2 = 0,25m1 gắn vào m1 nên khi đó ta sẽ vó VTCB mới O’ dịch xuống dưới so với O 1 đoạn bằng:
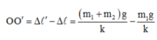

+ Khi về đến O thì m2 tuột khỏi m1 khi đó hệ chỉ còn lại m1 dao động với VTCB O, gọi biên độ khi đó là A1.
+ Vận tốc tại điểm O tính theo biên độ A’ bằng vận tốc cực đại của vật khi có biên độ là A1
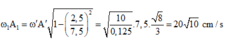
+ Biên độ dao động của m1 sau khi m2 tuột là: A 1 = 20 10 10 0 . 1 = 2 10 ≈ 6 , 32 c m

Đáp án A
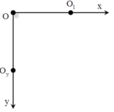
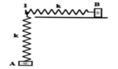
Chọn trục Ox nằm ngang, trục Oy thẳng đứng. Gốc O là vị trí gắn hai vật. O1 là VTCB của vật 1, O2 là VTCB của vật 2.
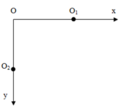
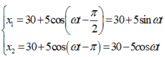
=> Khoảng cách của hai vật trong quá trình dao động:
![]() =
=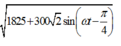
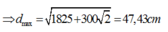

Chọn C.
Gắn trục Oxy vào hệ, gốc tạo độ O ≡ I
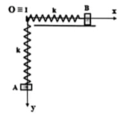

= 40 + 10 cos ω t + π 2 + 30 + 5 cos ω t 2

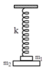

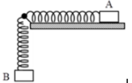

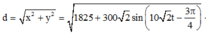
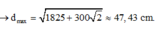

Đáp án C
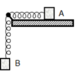
Tần số góc dao động điều hòa của hệ lò xo và hai vật ω = k 2 m = 100 2.0 , 2 = 5 10
→ Độ giãn của lò xo tại vị trí cân bằng Δ l 0 = g ω 2 = 4 c m
+ Từ vị trí cân bằng, nâng vật đến vị trí lò xo có chiều dài 48 cm rồi thả nhẹ →hai vật sẽ dao động với biên độ A 1 = 6 c m .
+ Phương trình động lực học cho vật m 2 trong quá trình vật chuyển động T – P 2 = m 2 a → tại vị trí vật m2 rời khỏi vật m 1 thì T = 3 , 5 N → m / s 2 (ta chú ý rằng gia tốc cực đại của dao động trên là a m a x = 15 m / s 2 ).
→ Tại vị trí m 2 rời khỏi vật m 1 , ta có x 0 = A 2 = 3 v 0 = 3 2 v m a x = 15 30
+ Sau khi m 2 rời khỏi m 1 , m 1 sẽ dao động điều hòa quanh vị trí cân bằng mới O' ở trên vị trí cân bằng cũ O một đoạn 2 cm → x 1 = 3 + 2 = 5 v 1 = v 0 = 15 30 , tần số dao động mới ω ' = k m = 100 0 , 2 = 10 5 rad/s
→ Biên độ dao động mới A 2 = 5 2 + 15 30 10 5 2 = 6 , 2 cm