Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(P=UI\cos\varphi\)
=> \(I=\frac{P}{U\cos\varphi}=\frac{P_i+I^2r}{U\cos\varphi}=\frac{80+I^2.32}{220.0.8}\)
=> phương trình bậc 2 của I và bấm máy tính
\(I_1=5\)(loại vì hiệu suất \(H=\frac{80}{UI\cos\varphi}=9,09\%\))
hoặc \(I_2=0.5\) (chọn)
=> \(I_0=I\sqrt{2}=0,5\sqrt{2}A.\)
chọn đáp án D.

Bạn tham khảo một bài tương tự ở đây nhé.
Câu hỏi của trần thị phương thảo - Học và thi online với HOC24

Đáp án D

Đáp án B
Sử dụng lí thuyết về công suất của mạch xoay chiều
Cách giải:
Công suất tiêu thụ của động cơ P = UIcosφ = 80W
Công suất tỏa nhiệt ∆P trên dây quấn là công suất hao phí nên hiệu suất của động cơ
H = P - ∆ P P = 1 - 8 80 = 0 , 9 ( 90 % )

Cường độ dòng hiệu dụng qua mỗi cuộn dây là \(I\)
Công suất động cơ: \(P=3.U.I\cos\varphi\Rightarrow I = \dfrac{P}{3.U\cos\varphi}=5A\)

Công suất tiêu thụ điện của động cơ: \(P=U.I.\cos\varphi=220.0,5.0,8=88W\)
Công suất có ích là: \(P_i=P-P_{hp}=88-11=77W\)
Hiệu suất: \(H=\dfrac{P_i}{P}=\dfrac{77}{88}=87,5\)%
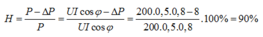
Đáp án B
+ Khi mắc lần lượt các linh kiện vào điện áp xoay chiều
Suy ra giá trị điện trở, cảm kháng và dung kháng của mạch
+ Khi mắc nối tiếp các linh kiện rồi mắc vào điện áp