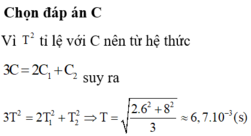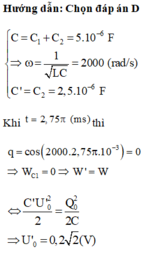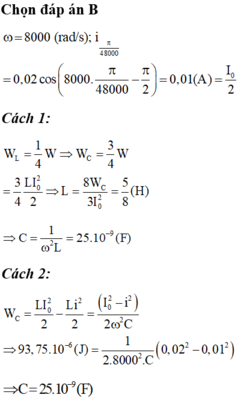Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(T = 1/f = 0,001s.\)
\(W_L = \frac{1}{2}W_{Lmax}=> \frac{1}{2}Li^2= \frac{1}{2}\frac{1}{2}LI_0^2.\)
=> \(i= \pm \frac{I_0}{\sqrt{2}}.\)
Thời gian để năng lượng từ trường lại bằng một nửa giá trị cực đại của nó là
\(\cos \varphi_1 = \frac{I_0/\sqrt{2}}{I_0}= \frac{1}{\sqrt{2}}=> \varphi _1= \frac{\pi}{4}=> \varphi = \frac{\pi}{2}.\)
\(t = \frac{\varphi}{\omega}= \frac{\pi/2}{2\pi/T}= \frac{T}{8}=2,5.10^{-4}s.\)

Đáp án C
+ ZL = wL = 160 W; ZC = 100 W ®
![]() W
W
®  A
A
+ Vì mạch có ZL > ZC nên u nhanh pha hơn i với
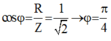
+ Biểu thức của dòng điện là:
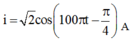
+ Thay t = 30 ms vào biểu thức của i ta được i = 1 A.

Đáp án A
Phương pháp: Sử dụng công thức tính chu kì
Cách giải:Khi dao động trong mạch LC có tần số góc ω thì năng lượng trong tụ hay cuộn cảm biến thiên vớitần số
![]()
Cứ sau mỗi thời gian t/2 thì năng lượng trong tụ bằng năng lượng trong cuộn cảm
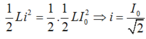
Tức là khoảng thời gian
![]()
![]()

Chọn đáp án B
ω = 8000 (rad/s); i π 48000 = 0,02 cos 8000. π 48000 − π 2 = 0,01 ( A ) = I 0 2 C 1 : W L = 1 4 W ⇒ W C = 3 4 W = 3 4 L I 0 2 2 ⇒ L = 8 W C 3 I 0 2 = 5 8 ( H ) ⇒ C = 1 ω 2 L = 25.10 − 9 ( F ) C 2 : W C = L I 0 2 2 − L i 2 2 = I 0 2 − i 2 2 ω 2 C ⇒ 93,75.10 − 6 ( J ) = 1 2.8000 2 . C 0,02 2 − 0,01 2 ⇒ C = 25.10 − 9 ( F )