Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)
Gọi x là số lượng khách từ người thứ 11 trở lên của nhóm (x>0)
Giá vé khi có thêm x khách là: \(800{\rm{ }}000 - 10{\rm{ }}000.x\)(đồng/người)
Doanh thu khi thêm x khách là:
\(\left( {x + 10} \right).\left( {800000 - 10000x} \right)\)\( = 10000\left( {x + 10} \right)\left( {80 - x} \right)\) (đồng)
b)
Chi phí thực sau khi thêm x vị khách là: 700 000(x+10) (đồng)
Lợi nhuận khi thêm x vị khách là:
\(T = 10000\left( {x + 10} \right)\left( {80 - x} \right)\)\( - 700000\left( {x + 10} \right)\)
\(\begin{array}{l} = 10000\left( {x + 10} \right).\left[ {80 - x - 70} \right]\\ = 10000\left( {x + 10} \right)\left( {10 - x} \right)\end{array}\)
Để công ty không bị lỗ thì lợi nhuận lớn hơn hoặc bằng 0
\(\begin{array}{l} \Leftrightarrow 10000\left( {x + 10} \right)\left( {10 - x} \right) \ge 0\\ \Leftrightarrow - 10 \le x \le 10\end{array}\)
Khi đó số khách du lịch tối đa là \(x + 10 = 10 + 10 = 20\) người thì công ty không bị lỗ.

a)
Do x là số lượng khách thứ 51 trở lên nên x>0.
Cứ thêm 1 người thì giá còn (300000-5 000.1) đồng/người cho toàn bộ hành khách.
Thêm x người thì giá còn (300 000-5 000.x) đồng/người cho toàn bộ hành khách.
Doanh thu theo x: \(\left( {50 + x} \right).\left( {300000 - 5000x} \right)\) (VNĐ)
b) Do chi phí thực sự cho chuyến đi là 15 080 000 đồng nên để công ty không bị lỗ thì doanh thu phải lớn hơn hoặc bằng 15 080 000 đồng
Khi đó:
\(\begin{array}{l}\left( {50 + x} \right).\left( {300000 - 5000x} \right) \ge 15080000\\ \Leftrightarrow \left( {50 + x} \right).5000.\left( {60 - x} \right) \ge 15080000\\ \Leftrightarrow \left( {x + 50} \right)\left( {60 - x} \right) \ge 3016\\ \Leftrightarrow - {x^2} + 10x + 3000 \ge 3016\\ \Leftrightarrow - {x^2} + 10x - 16 \ge 0\\ \Leftrightarrow {x^2} - 10x + 16 \le 0\\ \Leftrightarrow \left( {x - 2} \right)\left( {x - 8} \right) \le 0\\ \Leftrightarrow 2 \le x \le 8\end{array}\)
Vậy số người của nhóm du khách nhiều nhất là 58 người.

Gọi số khách tối đa đó là m
\(\Rightarrow\)Giá vé giảm cho mỗi người là: \(\left(m-40\right).5000\) đồng
\(\Rightarrow\) Giá vé giảm cho m người là: \(m\left(m-40\right)5000=\left(m^2-40m\right).5000\) đồng
Do số tiền này ko được vượt quá 7tr nên:
\(\left(m^2-40m\right).5000\le7000000\)
\(\Leftrightarrow m^2-40m-1400\le0\)
\(\Rightarrow20-30\sqrt{2}\le m\le20+30\sqrt{2}\)
Vậy số m tối đa là 62 người

Sửa đề: giảm đi 100 lượt
Gọi số tiền cần tăng thêm của 1 cốc là x(nghìn đồng)
=>Giá 1 ly sau khi tăng là x+20
=>Số lượt khách sau khi tăng là 4000-100x
=>Tổng doanh thu là S=(20+x)(4000-100x)
S'=4000-100x+(20+x)(-100)=2000-200x=0
=>x=10
=>S đạt maxkhi x=10
=>giá 1 cốc trà sữa cần bán là 20+10=30(ngàn đồng)

gọi \(x\times100000\text{ là số tiền vé đã tăng}\)
khi đó \(\hept{\begin{cases}\text{Giá vé khi đó là : }100000\times\left(x+4\right)\\\text{số người trên xe khi đó là : }60-10\times x=10\times\left(6-x\right)\end{cases}}\)
khi đó tổng số tiền bán vé thu được là :
\(100000\times\left(x+4\right)\times10\times\left(6-x\right)=1.000.000\times\left(4+x\right)\times\left(6-x\right)\)
\(\le1.000.000\times\left(\frac{4+x+6-x}{2}\right)^2=25.000.000\)
dấu "=" xảy ra khi \(x+4=6-x\Leftrightarrow x=1\)

Chọn C
+ Gọi thời lượng công ty đặt quảng cáo trên sóng phát thanh là x (phút), trên truyền hình là y (phút). Chi phí cho việc này là:800.000x + 4.000.000y (đồng)
Mức chi này không được phép vượt qúa mức chi tối đa, tức:
800.000x+ 4.000.000y ≤ 16.000.000 hay x+ 5y-20 ≤ 0
Do các điều kiện đài phát thanh, truyền hình đưa ra, ta có:x ≥ 5 và y ≤ 4
Đồng thời do x; y là thời lượng nên x; y ≥ 0
Hiệu quả chung của quảng cáo là x+ 6y.
Bài toán trở thành: Xác định x; y sao cho:
M( x; y) = x + 6y đạt giá trị lớn nhất.
Với các điều kiện : 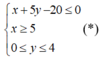
Trước tiên ta xác định miền nghiệm của hệ bất phương trình (*)
+Trong mặt phẳng tọa độ vẽ các đường thẳng
(d) : x + 5y - 20= 0 và (d’) ; x = 5; ( d’’) y = 4.
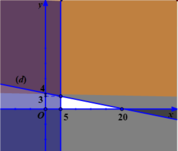
Khi đó miền nghiệm của hệ bất phương trình (*) là phần mặt phẳng(tam giác) không tô màu trên hình vẽ
Giá trị lớn nhất của M( x; y) =x+ 6y đạt tại một trong các điểm (5;3) ; ( 5;0) và ( 20; 0).
Ta có M (5; 3) = 23; M( 5; 0) = 5 và M( 20; 0) = 20.
+ Suy ra giá trị lớn nhất của M( x; y) bằng 23 tại ( 5; 3) tức là nếu đặt thời lượng quảng cáo trên sóng phát thanh là 5 phút và trên truyền hình là 3 phút thì sẽ đạt hiệu quả nhất.

Gọi x (đồng) là giá vé người lớn, y (đồng) là giá vé trẻ em (điều kiện x > 0, y > 0). Ta có hệ phương trình:
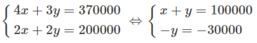
Suy ra y = 30000, x = 70000.
Vậy giá vé người lớn là 70 000 đồng, giá vé trẻ em là 30 000 đồng.


Khi chưa tăng tiền vé thì công ty thu được số tiền 1 tháng là:
50000 . 1000 = 50000000 đ = 50 triệu đồng
Khi tăng vé thì công ti thu được là:
(50000 + 10000) . 500 = 30000000 đ = 30 triệu đồng
Do đó mức giá là 50000đ/người là thích hợp đối với công ty
Nếu cách kia chưa hiểu thì làm cách này:
Vì ta có \(\frac{500}{1000}\) = \(\frac{1}{2}\) Vì khi tăng giá thì lượng khách giảm đi 1 nửa là 2 lần nên để số tiền thu được mỗi tháng lớn hơn hoặc là bằng số tiền ban đầu thì bắc buộc công ty phải tăng gia vé lên gấp 2 lần hoặc cao hơn....
Mà công ty chỉ tăng thêm \(\frac{10}{50}=\frac{1}{5}\) do đó mức giá ban đầu là thích hợp nhất