Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tham khảo:
a) Giả sử tàu xuất phát từ điểm O như hình dưới.
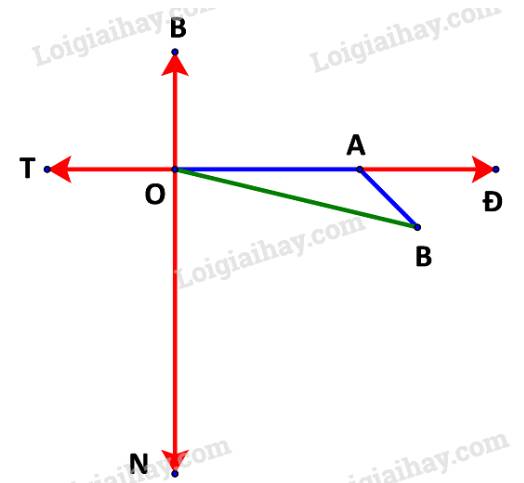
Trong 1 giờ, tàu di chuyển từ O đến A với quãng đường là: 20.1 =20 (km) tương ứng với 20 cm trên sơ đồ.
Trong 0,5 giờ tiếp theo, tàu di chuyển từ A đến B với quãng đường là: 20.0,5 = 10 (km) tương ứng với 10 cm trên sơ đồ.
b)
Trên sơ đồ, khoảng cách từ cảng đến tàu là đoạn OB dài khoảng 28 cm
Do đó khoảng cách từ cảng đến tàu thực tế khoảng 28 km.
c)
Nếu sau khi đi được 2 giờ, tàu chuyển sang hướng nam (thay vì hướng đông nam) thì sơ đồ đường đi của tàu như sau:
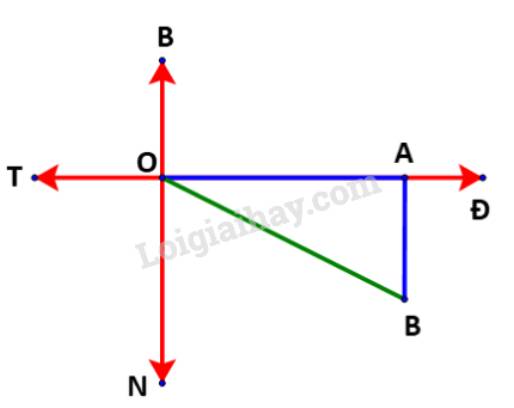
Sau 2 giờ đầu, tàu đi từ O đến A, với quãng đường là 20.2 = 40 (km) tương ứng 40 cm trên sơ đồ.
Sau đó, tàu chuyển sang hướng nam, vị trí của tàu là điểm B.
Khi đó ta có thể tính chính xác khoảng cách từ cảng đến tàu, chính là đoạn OB (do tam giác OAB vuông tại A) dựa vào định lí Pythagore: \(OB = \sqrt {O{A^2} + A{B^2}} \)

Tham khảo:
a) Ta có sơ đồ đường đi như sau:
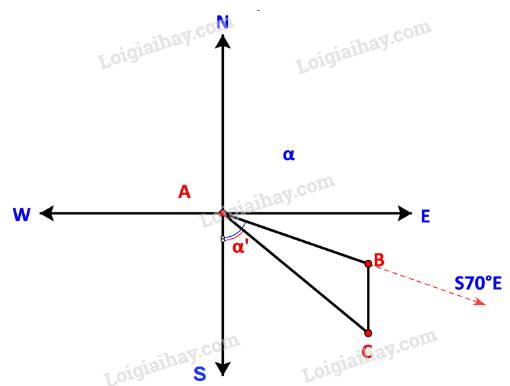
Trong đó: B là nơi động cơ bị hỏng, C là ví trí neo đậu của tàu trên hòn đảo.
Khoảng cách từ cảng A tới đảo nơi tàu neo đậu là đoạn AC.
Quãng đường tàu đi được sau 90 phút hay 1,5 giờ (ngay trước khi hỏng động cơ) là:
70.1,5 = 105 (km) hay AB = 105.
Sau 2 giờ tàu trôi tự do từ B đến C với vận tốc 8km/h , suy ra BC= 8.2 = 16 (km).
Ban đầu tàu di chuyển theo hướng \(S{70^o}E\) nên \(\widehat {BAS} = {70^o}\). Sau khi động cơ bị hỏng, tàu trôi theo hướng Nam do đó BC song song với AS.
\( \Rightarrow \widehat {ABC} = {180^o} - \widehat {BAS} = {110^o}\)
Áp dụng định lí cosin cho tam giác ABC ta có:
\({AC^2} = {BC^2} + {AB^2} - 2.AC.BC.\cos B\)
\(\begin{array}{l} \Rightarrow {AC^2} = {16^2} + {105^2} - 2.16.105.\cos {110^o} \approx 12430\\ \Rightarrow AC \approx 111,5.\end{array}\)
Vậy khoảng cách từ cảng A tới đảo nơi tàu neo đậu là khoảng 111,5 km.
b)
Theo sơ đồ, hướng từ cảng A tới đảo nơi tàu neo đậu là \(S{\alpha ^o}E\) với \({\alpha ^o} = \widehat {CAS}\).
Do BC // AS nên \(\widehat {CAS}= \widehat {ACB}\)
Áp dụng định lí sin cho tam giác ABC ta có:
\(\frac{BC}{{\sin A}} = \frac{AC}{{\sin B}} = \frac{AB}{{\sin C}}\)\( \Rightarrow \sin C = \frac{{AB.\sin B}}{AC}\)
Mà \(\widehat B = {110^o}\); \(AC \approx 111,5\); AB = 105.
\(\begin{array}{l} \Rightarrow \sin C= \frac{{105.\sin {{110}^o}}}{{111,5}} \approx 0,885\\ \Rightarrow \widehat C \approx {62^o}(do\;\widehat C < {90^o})\end{array}\)
Vậy hướng từ cảng A tới đảo nơi tàu neo đậu là \(S{62^o}E\).

a)
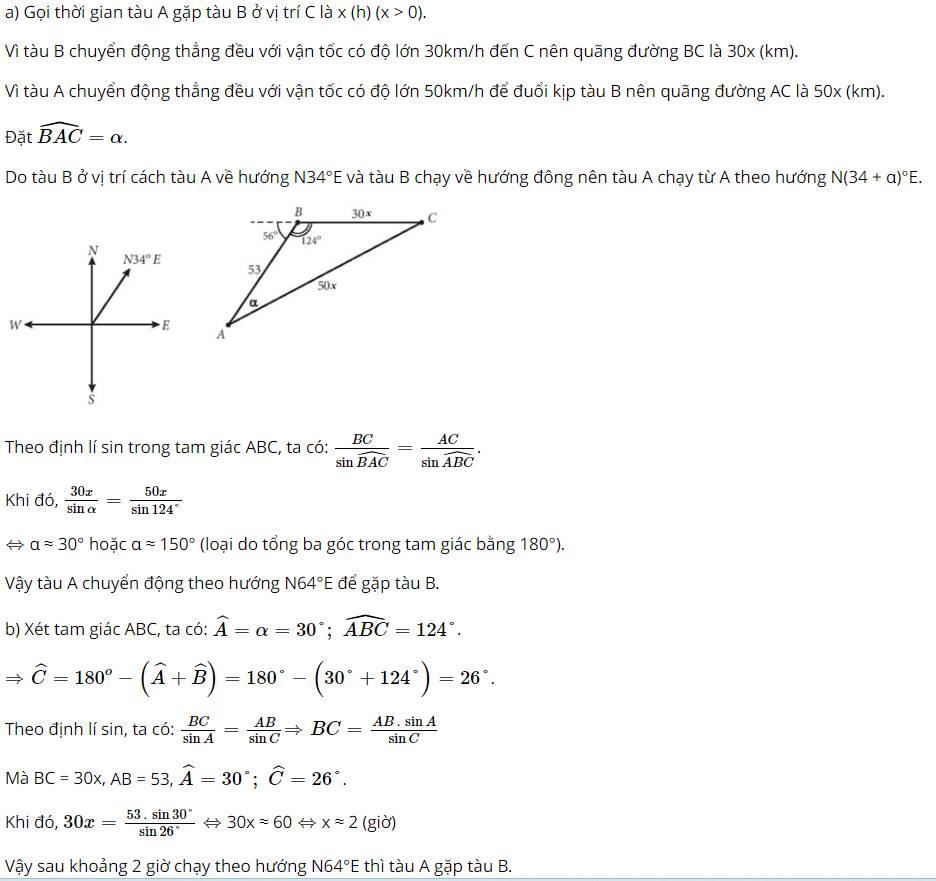
Gọi t (đơn vị: giờ) là thời gian đi cho đến khi hai tàu gặp nhau tại C.
Tàu B đi với vận tốc có độ lớn 30km/h nên quãng đường BC = 30t
Tàu A đi với vận tốc có độ lớn 50km/h nên quãng đường AC = 50t
Theo định lí sin, ta có: \(\frac{a}{{\sin \alpha }} = \frac{b}{{\sin B}}\)
Trong đó: \(\left\{ \begin{array}{l}a = BC = 30t\\b = AC = 50t\\\widehat B = {124^o}\end{array} \right.\)
\(\begin{array}{l} \Rightarrow \frac{{30t}}{{\sin \alpha }} = \frac{{50t}}{{\sin {{124}^o}}}\\ \Leftrightarrow \sin \alpha = \frac{{30t.\sin {{124}^o}}}{{50t}} = \frac{{30.\sin {{124}^o}}}{{50}} \approx 0,4974\end{array}\)
\( \Leftrightarrow \alpha \approx {30^o}\) hoặc \(\alpha \approx {150^o}\)(loại)
Vậy tàu A chuyển động theo hướng tạo với vị trí ban đầu của tàu B góc \({30^o}\).
b) Xét tam giác ABC, ta có:
\(\begin{array}{l}\widehat B = {124^o};\widehat A = {30^o}\\ \Rightarrow \widehat C = {180^o} - \left( {\widehat B + \widehat A} \right) = {180^o} - \left( {{{124}^o} + {{30}^o}} \right) = {26^o}\end{array}\)
Theo định lí sin, ta có
\(\frac{a}{{\sin A}} = \frac{c}{{\sin C}} \Rightarrow a = \frac{{c.\sin A}}{{\sin C}}\)
Mà \(\left\{ \begin{array}{l}a = BC = 30t\\c = AB = 53\\\widehat A = {30^o};\widehat C = {26^o}\end{array} \right. \Rightarrow 30t = \frac{{53.\sin {{30}^o}}}{{\sin {{26}^o}}}\)
\(\begin{array}{l} \Leftrightarrow 30t \approx 60,45\\ \Leftrightarrow t \approx 2\;(h)\end{array}\)
Vậy sau khoảng 2 giờ thì tàu A đuổi kịp tàu B.

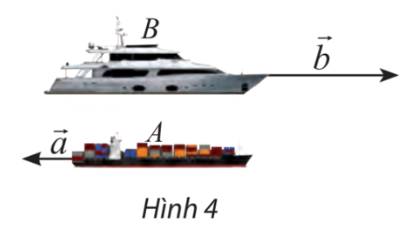
Ta thấy hai hướng đông và tây là ngược nhau và tỉ số độ dài \(\frac{{\left| {\overrightarrow b } \right|}}{{\left| {\overrightarrow a } \right|}} = \frac{{50}}{{20}} = \frac{5}{2}\)
\( \Rightarrow \overrightarrow b = - \frac{5}{2}\overrightarrow a \)


Chọn C.
Sau 2h quãng đường tàu thứ nhất chạy được là: S1 = 30.2 = 60km
Sau 2h quãng đường tàu thứ hai chạy được là: S2= 40.2 = 80 km
Suy ra sau 2h hai tàu cách nhau là:
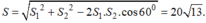

Sau 2h tàu thứ nhất ở vị trí B cách A là: \(2.30=60\left(km\right)\)
Tàu thứ 2 ở vị trí C cách A là: \(2.40=80\left(km\right)\)
Áp dụng định lý hàm cos:
\(BC=\sqrt{AB^2+AC^2-2AB.AC.cos60^0}=20\sqrt{13}\approx72,1\left(km\right)\)

Tham khảo:
Gọi B, C lần lượt là vị trí của tàu thứ nhất và tàu thứ hai sau 2,5 giờ.
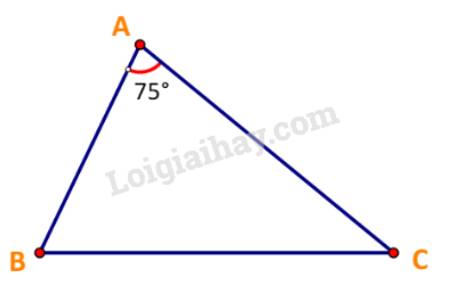
Sau 2,5 giờ:
Quãng đường tàu thứ nhất đi được là: AB = 8.2,5 = 20 (hải lí)
Quãng đường tàu thứ hai đi được là: AC = 12.2,5 = 30 (hải lí)
Áp dụng định lí cosin trong tam giác ABC ta có:
\(B{C^2} = A{C^2} + A{B^2} - 2.AC.AB.\cos A\)
\(\begin{array}{l} \Rightarrow B{C^2} = {30^2} + {20^2} - 2.30.20.\cos {75^o}\\ \Rightarrow B{C^2} \approx 989,4\\ \Rightarrow BC \approx 31,5\end{array}\)
Vậy hai tàu cách nhau 31,5 hải lí.

Sau 2 giờ, tàu thứ nhất đã đi được `25.2 = 50` hải lý.
Sau 2 giờ, tàu thứ hai đã đi được `20.2 = 40` hải lý.
Với a = `50` hải lý, b = `40` hải lý và `C = 180° - (15° + 32°) = 133°`, ta có:
`c^2 = 50^2 + 40^2 - 2.50.40.cos(133°)`
=> `c^2 ≈ 2500 + 1600 - 4000.(-0.6428) ≈ 4107.14`
Vậy, khoảng cách giữa hai tàu sau 2 giờ là:
`c ≈ √4107.14 ≈ 64,07 hải lý`
Tham khảo:
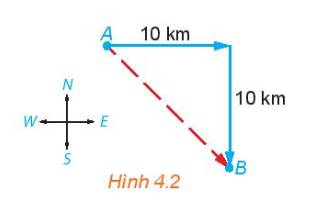
Gọi C là điểm mà tại đó tàu đổi từ hướng đông sang hướng Nam
Xét tam giác ABC ta có:
\(AC = BC = 10\;\left( {km} \right)\)
\( \Rightarrow \Delta ABC\) vuông cân tại C.
\( \Leftrightarrow \widehat A = {45^o}\)
Vậy con tàu phải đi theo hướng đông nam, góc \({45^o}\) so với hướng Đông.
Quãng đường con tàu phải đi là: \(AB = AC.\sqrt 2 = 10.\sqrt 2 \; \approx 14,142\;\left( {km} \right)\)