Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Theo công thức độc lập thì biên độ thỏa mãn
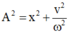
Thay số ta có:
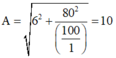

Tần số góc: \(\omega=\sqrt{\dfrac{k}{m}}=\sqrt{\dfrac{100}{0,1}}=10\pi(rad/s)\)
Biểu diễn dao động bằng véc tơ quay, tại thời điểm 7/60s thì véc tơ quay đã quay 1 góc là: \(\alpha=\omega.t=\dfrac{7}{6}\pi\)
Tại vị trí \(W_đ=3.W_t\)\(\Rightarrow W=W_đ+W_t=4W_t\)
\(\Rightarrow x=\pm\dfrac{A}{2}=\pm 2cm\)
Vì tốc độ của vật đang giảm nên có 2 trường hợp:
+ TH1: Dao động ứng với trạng thái tại M, sau khi quay \(\dfrac{7}{6}\pi\) sẽ đến biên âm --> Li độ là -4cm.
+ TH2: Dao động ứng với trạng thái N, sau khi quay \(\dfrac{7}{6}\pi\) sẽ đến biên độ dương -> Li độ là 4cm.

Đáp án D.
Gọi x là khoảng cách từ điểm giữ cố định tới điểm treo cố định, l là chiều dài khi bắt đầu giữ của lò xo. Nên khi này, ta được lò xo mới thực hiện dao động của vật với chiều dài 1-x lấy n = A x
Tại thời điểm giữ lò xo thì thế năng của nó là W t = W n 2
Khi giữ lò xo, phần thế năng bị mất đi là

Ta thấy, khi giữ thì 1 lò xo mới dao động với biên độ k' thỏa mãn
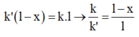
Bảo toàn cơ năng, ta có
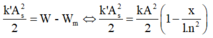
Do đó, ta có
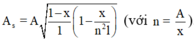
Giải ra được 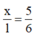

Chọn B
+ ω = k m = 1600 1 = 40 rad/s.
+ Truyền cho vật vận tốc 2 m/s tại vị trí cân bằng => vmax = ωA = 2 => A = 0,05m = 5cm.

Chọn đáp án A.
ω = k m = 100 0 , 1 = 10 10 ( r a d / s ) .
Mà A = 2 (cm) => v 0 = ω . A = 10 2 c m / s .
a 0 = ω 2 . A = 1000 2 c m / s 2
v v 0 2 + a a 0 2 = 1 ⇒ 10 10 10 20 2 + a 1000 2 2 = 1
⇒ a = 1000 ( c m / s 2 ) = 10 m / s 2 .

Đáp án A
Vận tốc cực đại của vật: v 0 = A . ω ⇒ v = v 0 3 = A . ω 3
Áp dụng công thức độc lập ta có:
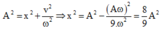
=> x = ± 2 2 3 A
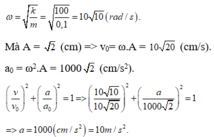

\(\text{ω}=\sqrt{\dfrac{100}{1}}=10\)
Ta có :
\(x^2+\dfrac{v^2}{\text{ω}^2}=A^2\Rightarrow x=5^2-\left(\dfrac{30}{10}\right)^2=4\)
Suy ra :
Độ lớn gia tốc : a = ωx = 4.10 = 40(cm2/s)