Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

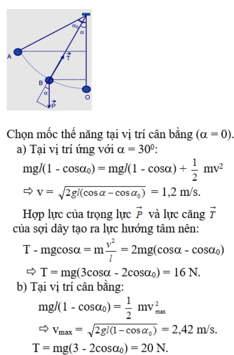
Vận tốc: \(v=\sqrt{2gl(\cos\alpha-\cos\alpha_0)}\)
Lực căng dây: \(T=mg(3\cos\alpha-2\cos\alpha_0)\)
bạn có thể cho mình biết là tại sao v và lực căng dây lại được tính như vậy được ko ?

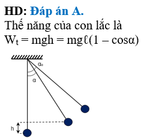
a) \(h=l-l\cos\alpha_0=1m\)
\(W=W_d+W_t=mgh=1J\)
b) Tính lực căng của dây treo khi vật qua vị trí cân bằng
Hai lực tác dụng vào vật: \(\overrightarrow{P},\overrightarrow{T}\)
Hợp lực: \(\overrightarrow{F}=\overrightarrow{P}+\overrightarrow{T}=m.\overrightarrow{a_{ht}}\)
\(m\frac{v^2_0}{l}=-P+T\)
\(T=m\frac{v^2_0}{l}+mg\)
\(T=3mg-2mg\cos\alpha_0=2N\)

Chọn mốc thế năng ở vị trí cân bằng
a. Ta có cơ năng
W = m g z = m g l ( 1 − cos 60 0 ) = 0 , 5.10.1 ( 1 − 0 , 5 ) = 2 , 5 ( J )
b. Theo định luật bảo toàn cơ năng
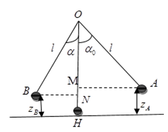
W A = W B ⇒ m g z A = 1 2 m v B 2 + m g z B ⇒ v B = 2 g ( z A − z B ) ( 1 ) M à z A = H M = l − O M = l − l cos α 0 z B = l − l cos α
Thay vào ( 1 ) ta có
v B = 2 g l ( cos α − cos α 0 ) + K h i α = 30 0 ⇒ v B = 2 g l ( cos 30 0 − cos 60 0 ) ⇒ v B = 2.10.1 ( 3 2 − 1 2 ) ≈ 2 , 71 ( m / s )
+ K h i α = 45 0 ⇒ v B = 2 g l ( cos 45 0 − cos 60 0 ) ⇒ v B = 2.10.1 ( 2 2 − 1 2 ) ≈ 2 , 035 ( m / s )
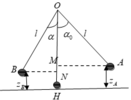
Xét tai B theo định luật II Newton ta có: P → + T → = m a →
Chiếu theo phương của dây
T − P y = m a h t ⇒ T − P cos α = m v 2 l ⇒ T − m g cos α = 2 m g ( cos α − cos α 0 ) ⇒ T = m g ( 3 cos α − 2 cos α 0 )
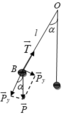
Khi α = 30 0 ⇒ T = m g ( 3 cos 30 0 − 2 cos 60 0 )
⇒ T = 0 , 5.10 ( 3. 3 2 − 2. 1 2 ) = 7 , 99 ( N )
Khi α = 45 0 ⇒ T = m g ( 3 cos 45 0 − 2 cos 60 0 )
⇒ T = 0 , 5.10 ( 3. 2 2 − 2. 1 2 ) = 5 , 61 N
Lưu ý: Khi làm trắc nghiệm thì các em áp dụng luôn hai công thức
+ Vận tốc của vật tại vị trí bất kỳ: v B = 2 g l ( cos α − cos α 0 )
+ Lực căng của sợi dây: T = m g ( 3 cos α − 2 cos α 0 )
c. Gọi C là vị trí để vật có v= 1,8m/s
Áp dụng công thức v C = 2 g l ( cos α − cos α 0 )
1 , 8 = 2.10.1 ( cos α − cos 60 0 ) ⇒ cos α = 0 , 662 ⇒ α = 48 , 55 0
Vật có đọ cao
z C = l − l cos α = 1 − 1.0 , 662 = 0 , 338 ( m )
d. Gọi D là vị trí vật có độ cao 0,18m
Áp dụng công thức
z D = l − l cos α ⇒ 0 , 18 = 1 − 1. cos α ⇒ cos α = 0 , 82
Áp dụng công thức
v D = 2 g l ( cos α − cos α 0 ) = 2.10.1. ( 0 , 82 − 0 , 5 ) = 2 , 53 ( m / s )
e. Gọi E là vị trí mà 2 w t = w đ Theo định luật bảo toàn cơ năng W A = W E
W A = W d E + W t E = 3 2 W d E ⇒ 2 , 5 = 3 2 . 1 2 . m v E 2 ⇒ v E = 2 , 5.4 3. m = 10 3.0 , 5 = 2 , 581 ( m / s )
f. Gọi F là vị trí để 2 w t = 3 w đ
Theo định luật bảo toàn cơ năng W A = W F
W A = W d F + W t F = 5 3 W t F ⇒ 2 , 5 = 5 3 . m g z F ⇒ z F = 2 , 5.3 5. m . g = 0 , 3 ( m ) M à z F = l − l cos α F ⇒ 0 , 3 = 1 − 1. cos α F ⇒ cos α F = 0 , 7 ⇒ α F = 45 , 573 0
Mặt khác v F = 2 g l ( cos α F − cos 60 0 ) = 2.10.1 ( 0 , 7 − 0 , 5 ) = 2 ( m / s )
Xét tại F theo định luật II Newton P → + T → = m a →
Chiếu theo phương của dây
− P cos α F + T F = m v F 2 l ⇒ − 0 , 5.10.0 , 7 + T F = 0 , 5. 2 2 1 ⇒ T = 5 , 5 ( N )

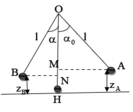
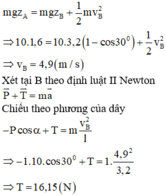

Vận tốc của vật ở vị trí góc bất kỳ là \(v = \sqrt{2gl(\cos \alpha - \cos \alpha_0)}\)
Lực căng dây tại một vị trí bất kỳ là: \(\tau = mg(3\cos \alpha - 2 \cos \alpha_0)\).
Bạn thay số vào là thu được kết quả.