Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Phương pháp: Sử dụng lí thuyết về dao động của con lắc đơn chịu tác dụng của lực điện trường
Cách giải:
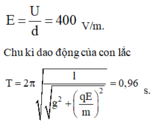
+ Cường độ điện trường giữa hai bản kim loại E = U/d
+ Gia tốc trọng trường hiệu dụng:
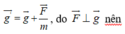
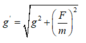
Mà
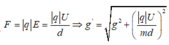
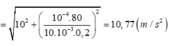
+ Chu kì dao động nhỏ của con lắc là:
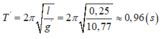
=> Chọn A

Đáp án A
Phương pháp: Sử dụng lí thuyết về dao động của con lắc đơn chịu tác dụng của lực điện trường
Cách giải:
+ Cường độ điện trường giữa hai bản kim loại E = U/d
+ Gia tốc trọng trường hiệu dụng:
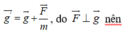
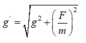
Mà
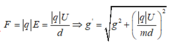
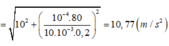
+ Chu kì dao động nhỏ của con lắc là:
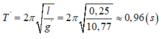
=> Chọn A

Đáp án C
Khi có điện trường con lắc lệch đến vị trí O’ lệch một góc α so với phương thẳng đứng.
Con lắc chịu tác dụng của trọng lực và lực điện.
→ tanα = 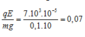
→ α = arctan 0,07 = 40.
Nếu kích thích thì vật dao động quanh vị trí O’, góc φmax = 80.
→ β = φmax - α = 40.
→ φmin = 00

Đây là bài toán con lắc đơn dao động trong lực lạ.
Hai bản tụ đặt thẳng đứng thì điện trường có phương nằm ngang, cường độ: \(E=\dfrac{U}{d}=\dfrac{100}{0,02}=5000(V/m)\)
Lực điện: \(F=q.E=20.10^{-6}.5000=0,1(N)\)
Trọng lực hiệu dụng: \(\vec{P'}=\vec{P}+\vec{F}\)
Do F vuông góc với P nên độ lớn: \(P'=\sqrt{P^2+F^2}=\sqrt{0,1^2+0,1^2}=0,1.\sqrt2\)
Trọng lực hiệu dụng: \(g'=\dfrac{P'}{m}=10\sqrt 2(m/s^2)\)
Ta có: \(T_0=2\pi\sqrt{\dfrac{l}{g}}\)
\(T=2\pi\sqrt{\dfrac{l}{g'}}\)
Suy ra: \(\dfrac{T_0}{T}=\sqrt{\dfrac{g'}{g}}=\sqrt{\sqrt{2}}=\sqrt[4]{2}\)
\(\Rightarrow T = \dfrac{1}{\sqrt[4]{2}}\) (s)



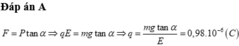
Theo giả thiết thì hai bản tụ đặt thẳng đứng trái dấu, nên ta có hình sau:
Góc lệch ở VTCB: \(\tan\alpha=\frac{F}{P}=\frac{qE}{mg}=\frac{qU}{mgd}=\frac{10^{-5}.400}{0,01.10.0,1}=0,4\)
\(\Rightarrow\alpha=21,8^0\)