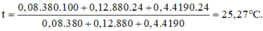Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




\(1cc=1ml=10^{-6}m^3\)
Khối lượng ban đầu của nước trong cốc: \(m_1=V_1.\rho_n=200kg\)
Khối lượng cốc: m = 300 – 200 = 100g
Nhiệt lượng do lượng nước thêm vào tỏa ra khi từ 100o đến 50o
\(Q_2=m_2.C_n\left(100-50\right)\)
Nhiệt lượng do lượng nước trong cốc thu vào để tăng từ 30o đến 50o
Q’ = m1.Cn(50 – 30 )
Nhiệt lượng do cốc thu vào khi tăng từ 30o đến 50o
\(Q_c=m.C_c\left(50-30\right)\)
Qtỏa = Qthu \(\Leftrightarrow\) Q' + Qc = Q2
\(\Leftrightarrow m.C_c\left(50-30\right)+m_1.C_n\left(50-30\right)=m_2.C_n\left(100-50\right)\)
\(\Rightarrow C=2100J/.Kg.K\)

Đáp án: B
Phương trình cân bằng nhiệt:
Qcốc + Qnước = Qthìa
↔ (mcốc.ccốc + mn.cn).(tcb – t1)
= mthìa.cthìa.(t2 – tcb)
↔ [(0,1.880) + (0,3.4,19.103)](t – 20)
= 0,075.380.(100 –t)
Giải ra ta được:
![]()

Gọi λ là nhiệt nóng chảy riêng của cục nước đá khối lượng m 0 ở t 0 = 0 ° C ; còn c 1 , m 1 , c 2 , m 2 là nhiệt dung riêng và khối lượng của cốc nhôm và của lượng nước đựng trong cốc ở nhiệt độ t 1 = 20 ° C. Nếu gọi t ° C là nhiệt độ của nước trong cốc nhôm khi cục nước đá vừa tan hết thì lượng nhiệt do cục nước đá ở t 0 = 0 ° C đã thu vào để tan thành nước ở t ° C bằng :
Q = λ m 0 + c 2 m 0 (t - t 0 ) = m 0 ( λ + c 2 t)
Còn nhiệt lượng do cốc nhôm và lượng nước đựng trong cốc ở t 1 = 20 ° C. toả ra để nhiệt độ của chúng giảm tới toC (với t < t 1 ) có giá trị bằng :
Q'= ( c 1 m 1 + c 2 m 2 )( t 1 - t)
Theo định luật bảo toàn năng lượng, ta có :
Q' = Q ⇒ ( c 1 m 1 + c 2 m 2 ) ( t 1 - t) = m 0 ( λ + c 2 t)
Từ đó suy ra :
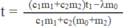
Thay số : t ≈ 3,7 ° C.

Gọi λ là nhiệt nóng chảy riêng của cục nước đá khối lượng m 0 , còn c 1 , m 1 , c 2 , m 2 là nhiệt dung riêng và khối lượng của cốc đồng và của lượng nước đựng trong cốc.
- Lượng nhiệt do cốc đồng và lượng nước đựng trong cốc ở t 1 = 25 ° C toả ra để nhiệt độ giảm tới t = 15,2 ° C có giá trị bằng :
Q = ( c 1 m 1 + c 2 m 2 ) ( t 1 -t)
- Lượng nhiệt do cục nước đá ở t 0 = 0 ° C thu vào để tan thành nước ở t = 15,2 ° C có giá trị bằng :
Q' = m 0 ( λ + c 2 t)
Theo nguyên lí cân bằng nhiệt, ta có :
Q' = Q ⇒ m 0 ( λ + c 2 t) = ( c 1 m 1 + c 2 m 2 ) ( t 1 -t)
Từ đó suy ra :
![]()
Thay số với chú ý m0 = 0,775 - 0,700 = 0,075 kg, ta tìm được :
![]()

Ta có:
Qtoa là nhiệt lượng mà sắt tỏa ra
Qthu là nhiệt lượng mà nước và nhôm nhận được để tăng nhiệt độ lên 800C và nhiệt lượng của 5g nước tăng từ 200C lên 1000C rồi hóa hơi
Khi quả cầu bắt đầu chạm vào m1=5g nước đã bốc hơi nên lượng nước tăng từ 200C lên 800C chỉ có
m′ = 100 − 5 = 95g
+ Q t o a = m F e c F e t - 80
+ Q t h u = m A l c A l 80 - 20 + m ' c n c 80 - 20 + m 1 c n c 100 - 20 + m 1 L
Theo phương trình cân bằng nhiệt, ta có:
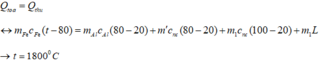
Đáp án: A

Nhiệt lượng tỏa ra:
Q C u = m C u . C C u t 2 − t = 75 1000 .380. 100 − t = 2850 − 28 , 5 t J
Nhiệt lượng thu vào:
Q H 2 O = m H 2 O . C H 2 O ( t − t 1 ) Q A l = m A l . C A l ( t − t 1 ) ⇔ = 300 1000 .4190. ( t − 20 ) = 1257. t − 25140 = 100 1000 .880. ( t − 20 ) = 88. t − 1760
Q t o a = Q t h u ↔ 2850 − 28 , 5 t = 1257. t − 25140 + 88. t − 1760 → t = 21 , 7 0 C
Đáp án: A

Khối lượng M của phần nước đá tan thành nước sau khi thả thỏi sắt nóng có nhiệt độ t ° C vào cốc nước đá ở 0 ° C được xác định bởi điều kiện cân bằng nhiệt:
M λ = cmt ⇒ M = cmt/ λ
trong đó λ là nhiệt nóng chảy riêng của nước đá, c là nhiệt dung riêng của thỏi sắt có khối lượng m.
Thay số, ta tìm được :
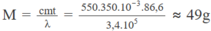

Gọi t là nhiệt độ khi có cân bằng nhiệt.
Nhiệt lượng do thìa đồng tỏa ra: Q 1 = m 1 c 1 ( t 1 - t )
Nhiệt lượng do cốc nhôm thu vào: Q 2 = m 2 c 2 ( t 2 - t )
Nhiệt lượng do nước thu vào: Q 3 = m 3 c 3 ( t 3 - t )
Phương trình cân bằng nhiệt: Q 1 = Q 2 + Q 3
⇔ m1c1(t1 - t) = m2c2(t - t2) + m3c3(t - t2)
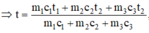
Thay số: