Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

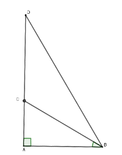
Từ giả thiết ra có chiều dài ban đầu của cây là AD; sau khi bị sét đánh thì cây còn lại AC = 1; C B A ^ = 40 0 và CD = CB
Xét tam giác ∆ ABC vuông tại A có BC = A C sin 40 o = 1,56m nên CD = 1,56m
Suy ra AD = AC + CD = 1 + 1,56 = 2,56m
Đáp án cần chọn là: D

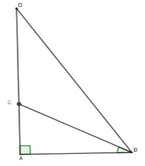
Từ giả thiết ra có chiều dài ban đầu của cây là AD; sau khi bị sét đánh thì cây còn lại AC = 1,5; C B A ^ = 35 0 và CD = CB
Xét tam giác ABC vuông tại A có BC = A C sin 35 o ≈ 2,6m
Suy ra AD = AC + CD = 1,5 + 2,6 = 4,1m
Vậy cây cao 4,1m
Đáp án cần chọn là: C

cây Hài Nam dài 4,5m
( Cho mình hỏi : cây Hài Nam là cây gì? )

Gọi tam giác tại bởi phần thân cây bị gãy với phần cây còn lại và mặt đất là △ ABC vuông tại A. Ta có
cos 20 = 7.5 / cạnh huyền
⇒ cạnh huyền = \(\dfrac{7,5}{cos20}\)\(\approx\) 8 ( m )
Áp dụng định lý Py-ta-go ta có:
phần bị gãy của cây cau là : \(\sqrt{8^2-7,5^2}\) = 2.78 ( m )
⇒ Chiều cao cây cau lúc đầu là : 8 + 2.78 =10.78 ( m )

Là \(\tan35^0\cdot5,5+\dfrac{5,5}{\cos35^0}\approx10,57\left(m\right)=1057\left(cm\right)\left(C\right)\)

Giả sử gốc là điểm A, điểm gãy là B và điểm ngọn chạm đất là C, ta có tam giác ABC vuông tại A
Trong đó \(AC=3m\) ; \(AB+BC=9\left(m\right)\)
Áp dụng định lý Pitago:
\(AB^2+AC^2=BC^2\)
\(\Rightarrow AB^2+3^2=\left(9-AB\right)^2\)
\(\Leftrightarrow9=81-18AB\)
\(\Rightarrow AB=4\left(m\right)\)
Vậy điểm gãy cách gốc 4m
Bài toán được mô tả như hình vẽ
∠ACB=40 độ là góc tạo bởi thân cây ngã xuống đất và mặt đất
AB=3m là phần khúc cây còn đứng
AB+BC là chiều cao của cây lúc đầu
Tam giác ABC vuông tại A
=>\(\sin\left(ACB\right)=\dfrac{AB}{BC}\Leftrightarrow BC=\dfrac{AB}{\sin\left(ACB\right)}=\dfrac{3}{\sin\left(40\right)}\approx4,67m\)
=> Chiều cao của cây lúc đầu là AB+BC=3+4,67=7,67(m)
(cái chỗ sin bạn tự kí hiệu góc vào nha