Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi O là tâm của hình bình hành ABCD; G = SO∩AM ⇒ G là trọng tâm ΔSAC ⇒ SG/SO = 2/3 ⇒ G cũng là trọng tâm ΔSBD
G ∈ AM ⊂ (P); G ∈ SO ⊂ (SBC) (1)
B' ∈ (P) và B' ∈ SB ⊂(SBC) (2)
D' ∈ (P) và D' ∈ SD ⊂(SBC) (3)
Từ (1); (2); (3) ⇒ G; B'; D' ∈ giao tuyến của (P) và (SBC)
Trong (SBC) vẽ BM//SO//DN (M, N ∈ B'D') ⇒ OG là đường trung bình của hình thang BDNM
⇒ BM + DN = 2OG = SG
Ta có :
x = SB/SB' = (SB' + BB')/SB' = 1 + BB'/SB' = 1 + BM/SG
y = SD/SD' = (SD' + DD')/SD' = 1 + DD'/SD' = 1 + DN/SG
⇒ x + y = 2 + (BM + DN)/SG = 2 + 1 = 3
1/x + 1/y = SB'/SB + SD'/SD = a/b
⇒ 3a/b = (x + y)(1/x + 1/y) ≥ 2√(xy).2√(1/xy) = 4
⇒ u = a/b ≥ 4/3 tối giản ⇒ GTNN của u = 4/3 xảy ra khi x = y ⇔ SB'SB' = SD/SD' ⇔ B'D'//BD

* Số phần tử của không gian mẫu: Ω = C 100 5 .
* Trong 100 sản phẩm đó có 8 sản phẩm hỏng và 92 sản phẩm không hỏng nên số phần tử của biến cố A là: n A = C 8 2 . C 92 3 .
Xác suất của biến cố A : P A = n A Ω = 299 6402 .
Chọn đáp án B.

\(\Delta_vABC\sim\Delta_vBCD\left(\widehat{BAC}=\widehat{CBD}\right)\) cùng phụ góc \(\widehat{ACB}\)
\(\Rightarrow\frac{AB}{BC}=\frac{BC}{CD}\Rightarrow BC=\sqrt{AB.CD}=a\)
Do MN là đường trung bình \(\Delta ABC\) \(\Rightarrow MN//AC\Rightarrow MN\perp BD\)
\(\Rightarrow BH=BN.cos\widehat{CBD}=\frac{1}{2}BC.\frac{BC}{BD}=\frac{1}{2}\frac{BC^2}{\sqrt{BC^2+CD^2}}=\frac{a\sqrt{5}}{5}\)
\(SH\perp\left(ABCD\right)\Rightarrow\widehat{SBH}=60^0\Rightarrow SH=BH.tan60^0=\frac{a\sqrt{15}}{5}\)
\(\left\{{}\begin{matrix}BD\perp SH\\BD\perp MN\end{matrix}\right.\) \(\Rightarrow BD\perp\left(SNH\right)\)
Từ H kẻ \(HK\perp SN\Rightarrow HK\) là đường vuông góc chung của SN và BD
\(\Rightarrow HK=d\left(SN;BD\right)\)
\(HN=\sqrt{BN^2-BH^2}=\frac{a\sqrt{5}}{10}\)
Áp dụng hệ thức lượng cho tam giác vuông SHN:
\(\frac{1}{HK^2}=\frac{1}{SH^2}+\frac{1}{NH^2}\Rightarrow HK=\frac{SH.NH}{\sqrt{SH^2+NH^2}}=\frac{a\sqrt{195}}{65}\)
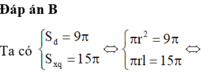


Đáp án B