Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng định luật khúc xạ
\(\sin i =n_t. \sin r_t\)=>\(\sin r_t = \frac{0,8}{n_t}=> r_t \approx 36,56^0\)
\(\sin i =n_d. \sin r_d\) => \(\sin r_d = \frac{0,8}{n_d}=> r_d \approx 36,95^0\)
Bề rộng quang phổ tạo ra dưới đáy bể là
\(TD = HD-HT = OH.(\tan r_d-\tan r_t) \approx 1,257 mm. \)

- Áp dụng định luật khúc xạ với tia đỏ và tia tím:
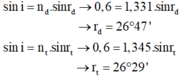
- Độ rộng vệt sáng dưới đáy bể là: 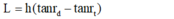
- Để hai vệt sáng đỏ và tím ở đáy bể hoàn toàn tách rời nhau thì độ rộng của chùm sáng không vượt quá giá trị:
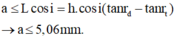

Đáp án B
Phương pháp: Định luật khúc xạ ánh sáng n1sini = n2sinr
Cách giải:
Áp dụng định luật khúc xạ với tia đỏ và tia tím:
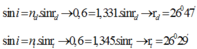
Độ rộng vệt sáng dưới đáy bể là:
![]()
Để hai vệt sáng đỏ và tím ở đáy bể hoàn toàn tách rời nhau thì độ rộng của chùm sáng không vượt quá giá trị:
![]()

Áp dụng định luật khúc xạ với tia đỏ và tia tím:
sini = nd.sinrd → 0,6 = 1.331.sinrd → rd = 26⁰47’
sini = nt.sinrt → 0,6 = 1.345.sinrt → rt = 26⁰29’
Độ rộng vệt sáng dưới đáy bể là: L = h(tanrd – tanrt)
Để hai vệt sáng đỏ và tím ở đáy bể hoàn toàn tách rời nhau thì độ rộng của chùm sáng không vượt quá giá trị: a ≤ Lcosi = h.cosi(tanrd – tanrt) = 5,06mm
Chọn đáp án B

Tia sáng Mặt Trời vào nước bị tán sắc và khúc xạ. Tia đỏ lệch ít nhất, tia tím lệch nhiều nhất.
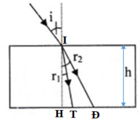
Ta có: tan i = 4/3 → i = 53,1o → sin i = 0,8
Áp dụng định luật khúc xạ tại I ta có: sin i = nđ. sin r2 = nt. sin r1
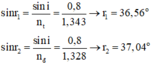
Xét tam giác vuông IHT, ta có: tan r1 = HT/IH ⇒ HT = h. tan r1
Xét tam giác vuông IHĐ, ta có: tan r2 = HĐ/IH ⇒ HĐ = h. tan r2
Độ dài quang phổ do tia sáng tạo ở đáy bể là :
ΔD = HĐ – HT = h.(tan r2 – tan r1) = 1,2.(tan 37,04o – tan 36,56o) = 0,01568m = 1,568cm

Đáp án B
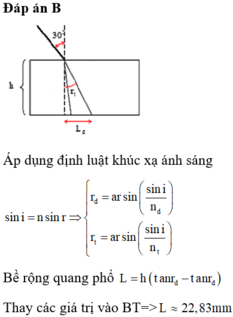
+ Áp dụng định luật khúc xạ ánh sáng
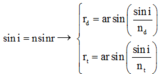
+ Bề rộng quang phổ : ![]()
→ Thay các giá trị vào biểu thức, ta thu được L = 22,83 mm.


Đáp án: C
Theo định luật khúc xạ, đối với tia đỏ sini = nđsinrđ => rđ = 36,97° đối với tia tím sini = ntsinrt => rt = 36,56°.
Theo hình vẽ, ta có:
HĐ = HItanrđ = 0,9032m
HT = HItanrt = 0,8898m
Bề rộng của dải quang phổ dưới đáy bể là:
ĐT = HĐ - HT = 1,34cm