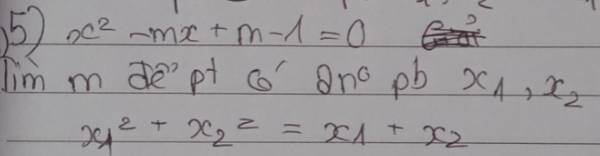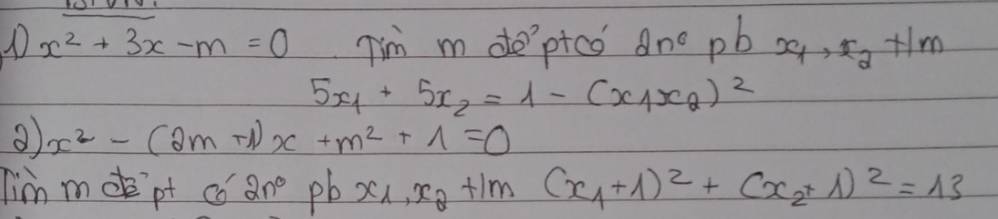Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




ĐK: \(x\ne\dfrac{\pi}{2}+k\pi\)
Ta có:
\(\left\{{}\begin{matrix}tanx=3\\sin^2x+cos^2x=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}sinx=3cosx\\9cos^2x+cos^2x=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}sinx=3cosx\\cos^2x=\dfrac{1}{10}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}sinx=3cosx\\cosx=\pm\dfrac{1}{\sqrt{10}}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}sinx=\dfrac{3}{\sqrt{10}}\\cosx=\dfrac{1}{\sqrt{10}}\end{matrix}\right.\\\left\{{}\begin{matrix}sinx=-\dfrac{3}{\sqrt{10}}\\cosx=-\dfrac{1}{\sqrt{10}}\end{matrix}\right.\end{matrix}\right.\)

5.
\(\Delta=m^2-4\left(m-1\right)=\left(m-2\right)^2\)
Pt có 2 nghiệm pb khi \(\left(m-2\right)^2>0\Rightarrow m\ne2\)
Khi đó theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=m\\x_1x_2=m-1\end{matrix}\right.\)
\(x_1^2+x_2^2=x_1+x_2\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=x_1+x_2\)
\(\Leftrightarrow m^2-2\left(m-1\right)=m\)
\(\Leftrightarrow m^2-3m+2=0\Rightarrow\left[{}\begin{matrix}m=1\\m=2\left(loại\right)\end{matrix}\right.\)
1.
\(\Delta=9+4m>0\Rightarrow m>-\dfrac{9}{4}\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-3\\x_1x_2=-m\end{matrix}\right.\)
\(5x_1+5x_2=1-\left(x_1x_2\right)^2\)
\(\Leftrightarrow5\left(x_1+x_2\right)=1-\left(x_1x_2\right)^2\)
\(\Leftrightarrow5.\left(-3\right)=1-\left(-m\right)^2\)
\(\Leftrightarrow m^2=16\Rightarrow\left[{}\begin{matrix}m=4\\m=-4< -\dfrac{9}{4}\left(loại\right)\end{matrix}\right.\)
2.
\(\Delta=\left(2m+1\right)^2-4\left(m^2+1\right)=4m-3>0\Rightarrow m>\dfrac{3}{4}\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2m+1\\x_1x_2=m^2+1\end{matrix}\right.\)
\(\left(x_1+1\right)^2+\left(x_2+1\right)^2=13\)
\(\Leftrightarrow x_1^2+2x_1+1+x_2^2+2x_2+1=13\)
\(\Leftrightarrow x_1^2+x_2^2+2\left(x_1+x_2\right)=11\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2+2\left(x_1+x_2\right)=11\)
\(\Leftrightarrow\left(2m+1\right)^2-2\left(m^2+1\right)+2\left(2m+1\right)=11\)
\(\Leftrightarrow2m^2+8m-10=0\)
\(\Rightarrow\left[{}\begin{matrix}m=1\\m=-5< \dfrac{3}{4}\left(loại\right)\end{matrix}\right.\)

khi bài toán bắt ta chứng minh một hình gì đó mà thiếu một ta hay một đường thẳng...

Xét \(\Delta HAB\) vuông tại H \(\left(AH\perp BC\right)\),ta có:
\(AB^2=AH^2+BH^2\left(ĐLPytago\right)\\ \Rightarrow BH^2=AB^2-AH^2\\ \Rightarrow BH=\sqrt{AB^2-AH^2}=\sqrt{7^2-2^2}=3\sqrt{5}\left(cm\right)\)
Xét \(\Delta ABC\) vuông tại A và có AH là đường cao \(\left(AH\perp BC\right)\),ta có:
\(AH^2=BH.CH\left(HTL\right)\\ \Rightarrow CH=\dfrac{AH^2}{BH}=\dfrac{2^2}{3\sqrt{5}}=\dfrac{4\sqrt{5}}{15}\left(cm\right)\)

ΔABC vuông cân tại A⇒AB=AC=4
Áp dụng hệ thức lượng ta có:
\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)
\(\Rightarrow\dfrac{1}{AH^2}=\dfrac{1}{4^2}+\dfrac{1}{4^2}\)
\(\Rightarrow\dfrac{1}{AH^2}=\dfrac{1}{16}+\dfrac{1}{16}\\ \Rightarrow\dfrac{1}{AH^2}=\dfrac{1}{8}\\ \Rightarrow AH^2=8\\ \Rightarrow AH=\sqrt{8}\)
Vì ΔABC vuông cân tại A
⇒ AB = AC = 4 cm
Áp dụng dịnh lí Py-ta-go vào ΔABC vuông tại A ta có:
BC2=AB2+AC2=42+42=32
⇔BC=\(4\sqrt{2}\)
Ta có:AB.AC=AH.BC (hệ thức lượng)
⇔\(AH=\dfrac{AB.AC}{BC}=\dfrac{4.4}{4\sqrt{2}}=2\sqrt{2}\left(cm\right)\)
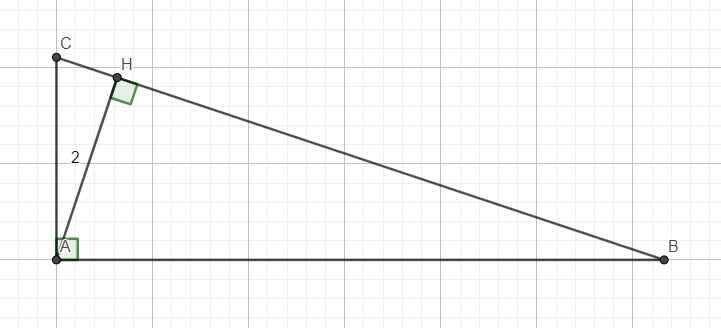
Cho tam giác ABC vuông tại A, AH vuông góc với BC,có AH=2, tan B=1/3. Tính AB, AC. Mong mn giúp mình

Trong tam giác vuông ABH ta có:
\(tanB=\dfrac{AH}{BH}\Rightarrow BH=\dfrac{AH}{tanB}=6\)
Áp dụng định lý Pitago:
\(AB^2=AH^2+BH^2=40\)
\(\Rightarrow AB=2\sqrt{10}\)
Trong tam giác vuông ABC:
\(tanB=\dfrac{AC}{AB}\Rightarrow AC=AB.tanB=\dfrac{2\sqrt{10}}{3}\)

Áp dụng định lý Pitago:
\(BC=\sqrt{AB^2+AC^2}=5\)
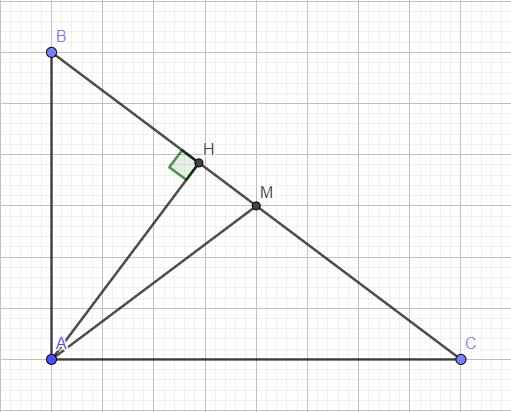
Trong tam giác vuông ABC, AM là trung tuyến ứng với cạnh huyền
\(\Rightarrow AM=\dfrac{1}{2}BC=\dfrac{5}{2}\)
Áp dụng hệ thức lượng:
\(AH.BC=AB.AC\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{12}{5}\)
Áp dụng định lý Pitago cho tam giác vuông AHM:
\(HM=\sqrt{AM^2-AH^2}=\dfrac{7}{10}\)
 mong mn giúp mình
mong mn giúp mình