K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
17 tháng 7 2021
câu 3
A1=110o(đối đỉnh)
A2+A4=180o(kề bù)
=>A2=70o
A3=70o
B3=55o(đối đỉnh)
B3+B1=180o(kề bù)
B1=125o
B4=125o(đối đỉnh)
VN
Tính:
\(A=2^{2012}-\left(2^{2011}+2^{2010}+...+2+1\right)\)
Giúp mk nốt bài này nha mọi ng. Mk cần 23h
0
VP
0
NN
1
20 tháng 8 2021
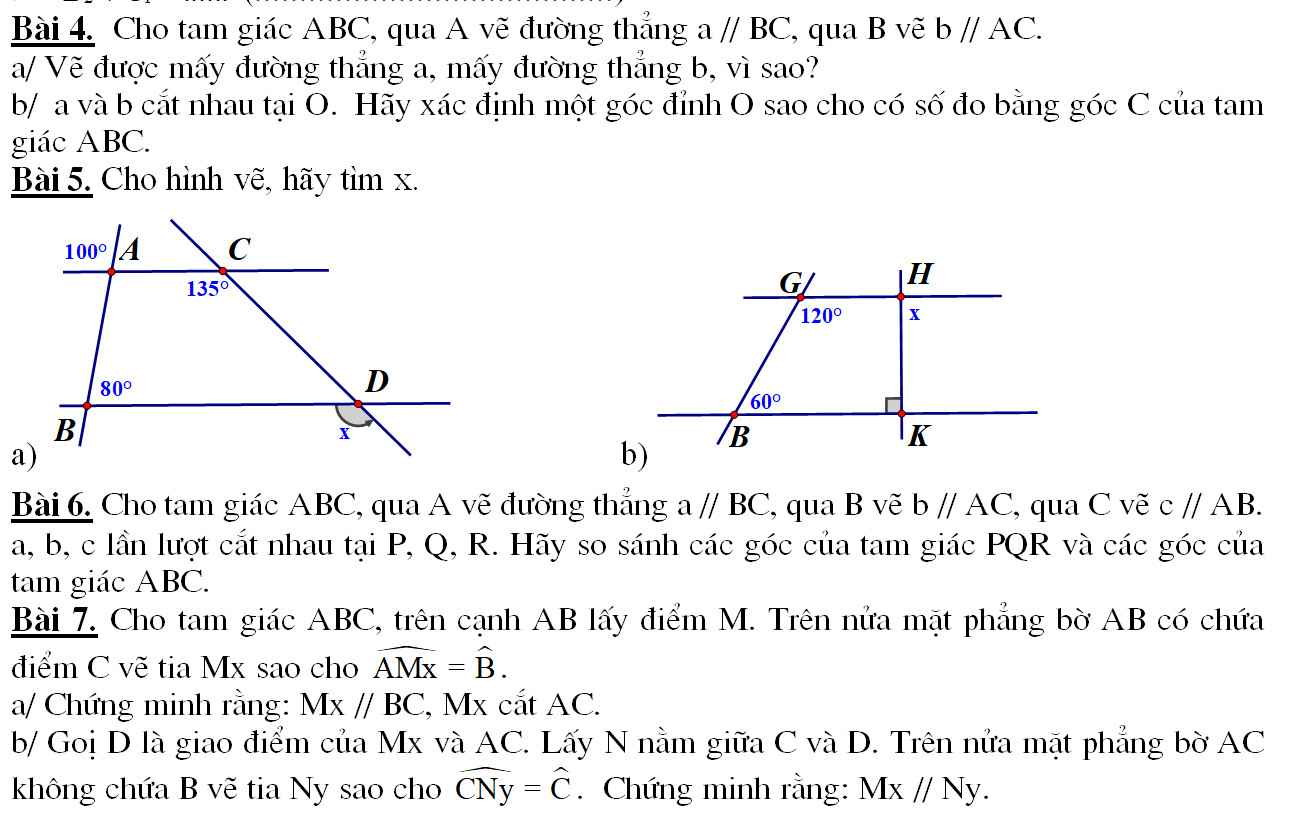
Bài 5:
Ta có : \(\widehat{A_1}+\widehat{A_3}=180^o\) (kề bù)
\(100^o+\widehat{A_3}=180^o\)
\(\widehat{A_3}=80^o\)
Ta có: \(\widehat{A_3}=\widehat{B_1}=80^o\)
\(\widehat{A_3}\) và \(\widehat{B_1}\) ở vị trí đồng vị
\(\Rightarrow AC//BD\)
\(\Rightarrow\widehat{C}_1=\widehat{D_1}=135^o\) (đồng vị)
\(x=135^o\)
b)
Ta có: \(\widehat{G_1}+\widehat{B_1}=180^o\left(120^o+60^o=180^o\right)\)
\(\widehat{G_1}\) và \(\widehat{B_1}\) ở vị trí trong cùng phía
\(\Rightarrow QH//BK\)
\(\Rightarrow\widehat{H_1}=\widehat{K_1}=90^o\)(so le)
\(x=90^o\)
PQ
12 tháng 11 2018
cảm ơn Nguyễn Thu Trang nha những ng đó hack nik tr khi olm đc đổi ms cơ lên....buồn
TN
30 tháng 12 2022
b) \(\left(x-1\right)^3=\dfrac{1}{8}\)
\(\left(x-1\right)^3=\left(\dfrac{1}{2}\right)^3\)
\(x-1=\dfrac{1}{2}\)
\(x=\dfrac{1}{2}+1\)
\(x=\dfrac{3}{2}\)
19 tháng 7 2019
b) Để g(x) có nghiệm
\(\Leftrightarrow\left(x-1\right)\left(2-3x\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-1=0\\2-3x=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=1\\x=\frac{2}{3}\end{cases}}\)
Vậy \(x\in\left\{1;\frac{2}{3}\right\}\)là nghiệm của đa thức g(x)
19 tháng 7 2019
c) Để k(x) có nghiệm
\(\Leftrightarrow x^2-3x-4=0\)
\(\Leftrightarrow x^2+x-4x-4=0\)
\(\Leftrightarrow x\left(x+1\right)-4\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(x-4\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x+1=0\\x-4=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=-1\\x=4\end{cases}}}\)
Vậy \(x\in\left\{-1;4\right\}\)là nghiệm của đa thức
\(9x^2-72x=0\)
\(\Leftrightarrow9x\left(x-8\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}9x=0\\x-8=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=0\\x=8\end{matrix}\right.\)
Vậy..
\(9x^2-72x=0\)
\(\Rightarrow9x.\left(x-8\right)=0\)
\(\Rightarrow\left\{{}\begin{matrix}9x=0\\x-8=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=0\\x=8\end{matrix}\right.\)
Vậy \(x\in\left\{0;8\right\}\)
Chúc bạn học tốt!!!