KB
3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
18 tháng 9 2020
Ta có: \(\frac{2000}{-2001}=-\frac{2000}{2001}=-\left(\frac{2001-1}{2001}\right)=-\left(\frac{2001}{2001}-\frac{1}{2001}\right)=-\left(1-\frac{1}{2001}\right)=-1+\frac{1}{2001}\)
\(-\frac{2003}{2002}=-\left(\frac{2002+1}{2002}\right)=-\left(\frac{2002}{2002}+\frac{1}{2002}\right)=-\left(1+\frac{1}{2002}\right)=-1-\frac{1}{2002}\)
Vì \(\frac{1}{2001}>-\frac{1}{2002}\) nên \(-1+\frac{1}{2001}>-1-\frac{1}{2002}\)
hay \(\frac{2000}{-2001}>-\frac{2003}{2002}\)
TN
1
DP
19 tháng 7 2017
\(x+\left(x+1\right)+\left(x+2\right)+....+\left(x+2003\right)=2004\)
\(\Leftrightarrow x+\left(x+x+....+x\right)+\left(1+2+....+2003\right)=2004\)
\(\Leftrightarrow x+2003x+2007006=2004\)
\(\Leftrightarrow2004x=2004-2007006\)
\(\Leftrightarrow2004x=-2005002\)
\(\Leftrightarrow x=-\frac{2001}{2}=-1000,5\)
8 tháng 7 2016
Do dãy 2000 số tự nhiên liên tiếp đó không có số nguyên tố nào nên chúng là hợp số.
Coi dãy đó chứa các số tự nhiên liên tiếp từ a + 2 đến a + 2001 \(\left(a\in N\right)\)
Để tất cả các số trên là hợp số thì a phải chia hết các số từ 2 đến 2001, vì vậy a = 2001!
Thế vào các số trên, ta có:
- a + 2 = 2001! + 2 = 2 ( 3 * 4 * 5 * ... * 2001 + 1 ) ( là hợp số ) - thoả mãn
- a + 3 = 2001! + 3 = 3 ( 2 * 4 * 5 * ... * 2001 + 1 ) ( là hợp số ) - thoả mãn
- a + 4 = 2001! + 4 = 4 ( 2 * 3 * 5 * ... * 2001 + 1 ) ( là hợp số ) - thoả mãn
...................................................................................................................................
- a + 2001 = 2001! + 2001 = 2001 ( 2 * 3 * 4 * ... * 2000 + 1 ) ( là hợp số ) - thoả mãn
Vậy trong tập hợp số tự nhiên, dãy có 2000 số tự nhiên liên tiếp mà không có 1 số nguyên tố nào là:
2001! + 2 ; 2001! + 3 ; 2001! + 4 ; .... ; 2001! + 1999 ; 2001! + 2000 ; 2001! + 2001
NN
1
20 tháng 8 2021
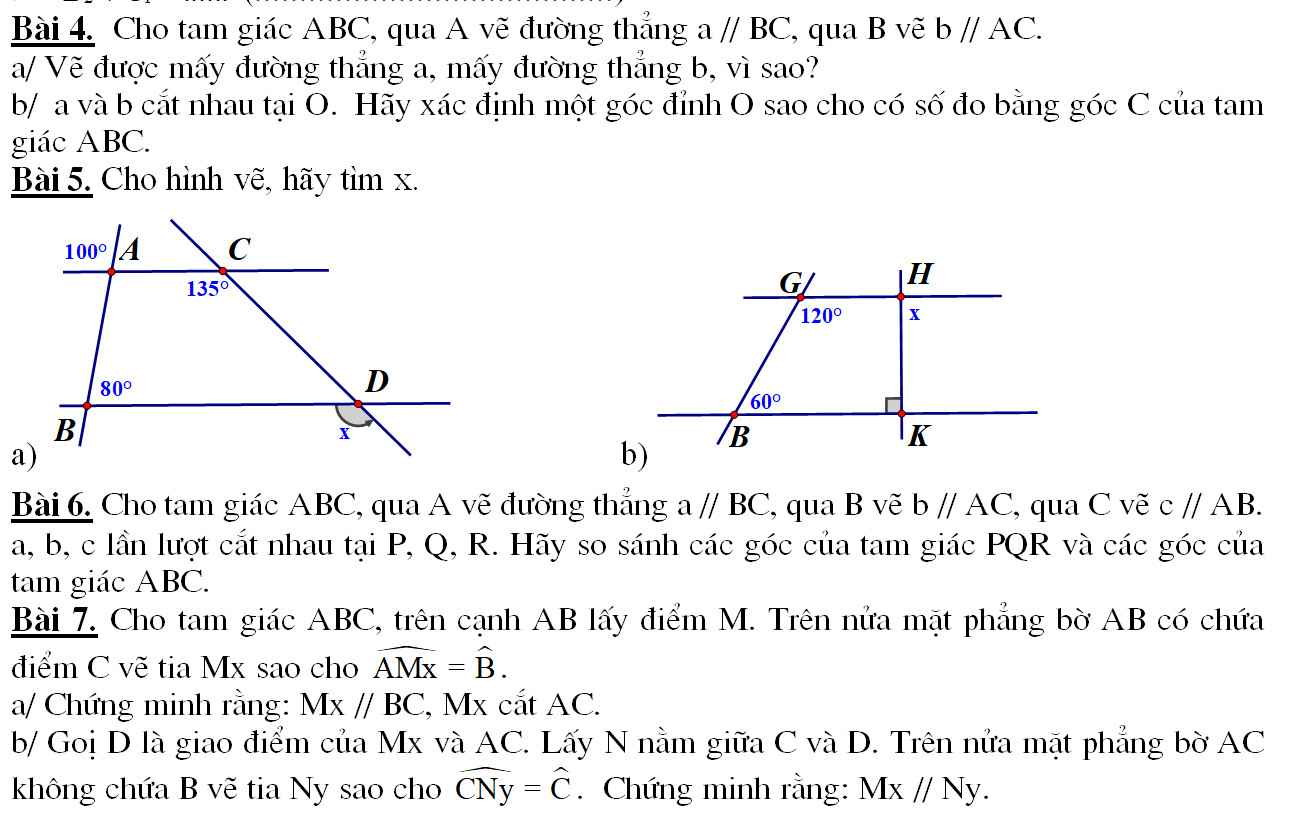
Bài 5:
Ta có : \(\widehat{A_1}+\widehat{A_3}=180^o\) (kề bù)
\(100^o+\widehat{A_3}=180^o\)
\(\widehat{A_3}=80^o\)
Ta có: \(\widehat{A_3}=\widehat{B_1}=80^o\)
\(\widehat{A_3}\) và \(\widehat{B_1}\) ở vị trí đồng vị
\(\Rightarrow AC//BD\)
\(\Rightarrow\widehat{C}_1=\widehat{D_1}=135^o\) (đồng vị)
\(x=135^o\)
b)
Ta có: \(\widehat{G_1}+\widehat{B_1}=180^o\left(120^o+60^o=180^o\right)\)
\(\widehat{G_1}\) và \(\widehat{B_1}\) ở vị trí trong cùng phía
\(\Rightarrow QH//BK\)
\(\Rightarrow\widehat{H_1}=\widehat{K_1}=90^o\)(so le)
\(x=90^o\)
17 tháng 11 2016
ta lấy 5 chữ số 1 cuối cùng chia cho 1001 ta đc: 11111:1001=11 dư 100
BV
3
13 tháng 4 2023
`7,`
`a, B+A=4x-2x^2+3`
`-> B=(4x-2x^2+3)-A`
`-> B=(4x-2x^2+3)-(x^2-2x+1)`
`B=4x-2x^2+3-x^2+2x-1`
`B=(-2x^2-x^2)+(4x+2x)+(3-1)`
`B=-3x^2+6x+2`
`b, C-A=-x+7`
`-> C=(-x+7)+A`
`-> C=(-x+7)+(x^2-2x+1)`
`-> C=-x+7+x^2-2x+1`
`C=x^2+(-x-2x)+(7+1)`
`C=x^2-3x+8`
`c,`
`A-D=x^2-2`
`-> D= A- (x^2-2)`
`-> D=(x^2-2x+1)-(x^2-2)`
`D=x^2-2x+1-x^2+2`
`D=(x^2-x^2)-2x+(1+2)`
`D=-2x+3`
13 tháng 4 2023
`6,`
`a,`
`P+Q=4x-2x^2+3`
`-> Q=(4x-2x^2+3)-P`
`-> Q=(4x-2x^2+3)-(3x^2+x-1)`
`Q=4x-2x^2+3-3x^2-x+1`
`Q=(-2x^2-3x^2)+(4x-x)+(3+1)`
`Q=x^2+3x+4`
`b,`
`x^2-5x+2-P=H`
`-> H= (x^2-5x+2)-(3x^2+x-1)`
`H=x^2-5x+2-3x^2-x+1`
`H=(x^2-3x^2)+(-5x-x)+(2+1)`
`H=-4x^2-6x+3`
`c,`
`P-R=5x^2-3x-4`
`-> R= P- (5x^2-3x-4)`
`-> R=(3x^2+x-1)-(5x^2-3x-4)`
`R=3x^2+x-1-5x^2+3x+4`
`R=(3x^2-5x^2)+(x+3x)+(-1+4)`
`R=-2x^2+4x+3`
187:2003=305651 (dư 3)
tích co mình nha
Bạn ơi, 1817 mà bạn?