Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(=\dfrac{x+2}{x+2}=1\)
b: \(=\dfrac{2x+6}{x+3}=2\)

Câu 1: A
Câu 2: B
Câu 3: D
Câu 4: A
Câu 5: C
Câu 6: B
Câu 7: A
Câu 9: B

\(5,\\ a,=x^4+4x^2+4-4x^2=\left(x^2+2\right)^2-4x^2=\left(x^2-2x+2\right)\left(x^2+2x+2\right)\\ b,=x^4+16x^2+64-16x^2=\left(x^2+8\right)^2-16x^2=\left(x^2-4x+8\right)\left(x^2+4x+8\right)\\ c,=x^8+x^7+x^6-x^6+x^5-x^5+x^4-x^4+x^3-x^3+x^2-x^2+x-x+1\\ =x^6\left(x^2+x+1\right)-x^4\left(x^2+x+1\right)+x^3\left(x^2+x+1\right)-x\left(x^2+x+1\right)+\left(x^2+x+1\right)\\ =\left(x^6-x^4+x^3-x+1\right)\left(x^2+x+1\right)\)
\(d,=x^8+2x^4+1-x^4=\left(x^4+1\right)^2-x^4=\left(x^4-x^2+1\right)\left(x^4+x^2+1\right)\\ =\left(x^4-x^2+1\right)\left(x^4+2x^2+1-x^2\right)\\ =\left(x^4-x^2+1\right)\left(x^2-x+1\right)\left(x^2+x+1\right)\\ e,=x^5+x^4-x^4+x^3-x^3+x^2-x^2+x+1\\ =x^3\left(x^2+x+1\right)-x^2\left(x^2+x+x\right)+\left(x^2+x+1\right)\\ =\left(x^3-x^2+1\right)\left(x^2+x+1\right)\\ f,=x^3+2x^2-x^2-2x+2x+4\\ =\left(x+2\right)\left(x^2-x+2\right)\\ g,=x^4+2x^2+1-25=\left(x^2+1\right)^2-25\\ =\left(x^2+1-5\right)\left(x^2-1-5\right)=\left(x^2-4\right)\left(x^2-6\right)=\left(x-2\right)\left(x+2\right)\left(x^2-6\right)\)
\(h,=x^3-2x^2+2x^2-4x+2x-4=\left(x-2\right)\left(x^2+2x+2\right)\\ i,=a^4-4a^2b^2+4b^4-4a^2b^2=\left(a^2-2b^2\right)^2-4a^2b^2\\ =\left(a^2-2ab-2b^2\right)\left(a^2+2ab-2b^2\right)\)

Hướng dẫn: A đạt GTLN khi \(\dfrac{1}{A}\) đạt GTNN
Ta có: \(x^2+2\ge0\forall x\)
\(\Rightarrow A=\dfrac{1}{x^2+2}\le\dfrac{1}{2}\forall x\)
Vậy GTLN của A là 1/2
=> A

a: Xét ΔEAD và ΔECG có
góc EAD=góc ECG
góc AED=góc CEG
=>ΔEAD đồng dạng với ΔECG
=>AD/CG=ED/EG
=>AD*EG=ED*CG
b: Xét ΔHEG và ΔHCB có
góc HEG=góc HCB
góc EHG=góc CHB
=>ΔHEG đồng dạng với ΔHCB
=>HE/HC=HG/HB
Xét ΔHAB và ΔHCG có
góc HAB=góc HCG
góc AHB=góc CHG
=>ΔHAB đồng dạng với ΔHCG
=>HA/HC=HB/HG
=>HC/HA=HG/HB
=>HC/HA=HE/HC
=>HC^2=HA*HE
c: HI//BA
=>HI/BA=CH/CA=CI/CB
HI//EG
=>HI/EG=BI/BC
HI/BA=CI/CB
HI/BA+HI/EG=BI/BC+CI/BC=1
=>HI(1/BA+1/EG)=1
=>1/BA+1/EG=1/HI

(x^2-6x+8)(x^2-8x+15)+1
=(x^2-4x-2x+8)(x^2-5x-3x+15)+1
=(x(x-4)-2(x-4))(x(x-5)-3(x-5))+1
=(x-4)(x-2)(x-5)(x-3)+1
=(x-2)(x-5)(x-3)(x-4)+1
=(x^2-7x+10)(x^2-7x+12)+1
Gọi a=x^2-7x+11, ta có
(a-1)(a+1)+1
= a2 - 1 + 1
= a2
= (x2 - 7x + 11)2

\(x^5+x^4+1\)
\(=x^5+x^4+x^3-x^3-x^2-x+x^2+x+1\)
\(=\left(x^5+x^4+x^3\right)-\left(x^3+x^2+x\right)+\left(x^2+x+1\right)\)
\(=x^3.\left(x^2+x+1\right)-x\left(x^2+x+1\right)+\left(x^2+x+1\right)\)
\(=\left(x^2+x+1\right)\left(x^3-x+1\right)\)
cảm ơn bạn nhiều, không biết còn cách không? Mong nhận đượ giúp đỡ!

1: Xét ΔABD vuông tại A và ΔDAC vuông tại D có
góc ABD=góc DAC
=>ΔABD đồng dạng với ΔDAC
2: ΔABD đồng dạng với ΔDAC
=>BD/AC=AB/DA=AD/DC
=>AD/16=BD/AC=18/DA
=>AD^2=16*18=288
=>AD=12căn 2(cm)
AC=căn AD^2+DC^2=4căn 82(cm)
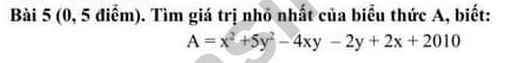










\(A=x^2-4xy+4y^2+2x-4y+1+y^2+2y+1+2008\)
\(A=\left(x-2y\right)^2+2\left(x-2y\right)+1+\left(y+1\right)^2+2008\)
\(A=\left(x-2y+1\right)^2+\left(y+1\right)^2+2008\ge2008\)
\(\Rightarrow A_{min}=2008\Leftrightarrow\left\{{}\begin{matrix}x-2y+1=0\\y+1=0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x=-3\\y=-1\end{matrix}\right.\)
mình cảm ơn ạ.