K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 4 2021
Đặt \(\int f\left(x\right)dx=F\left(x\right)\Rightarrow\int\limits^{17}_1f\left(x\right)dx=F\left(17\right)-F\left(1\right)\)
Từ giả thiết:
\(2x.f\left(x^2+1\right)+\dfrac{f\left(\sqrt{x}\right)}{2\sqrt{x}}=2lnx\)
Lấy nguyên hàm 2 vế:
\(F\left(x^2+1\right)+F\left(\sqrt{x}\right)=2xlnx-2x+C\)
Thay \(x=4\):
\(F\left(17\right)+F\left(2\right)=16ln2-8+C\) (1)
Thay \(x=1\):
\(F\left(2\right)+F\left(1\right)=-2+C\) (2)
Trừ vế cho vế (1) cho (2):
\(F\left(17\right)-F\left(1\right)=16ln2-6\)
Vậy \(\int\limits^{17}_1f\left(x\right)dx=16ln2-6\)
MT
3
TT
1
KV
25 tháng 1
= -2³/3 + 2²/2 + 2.2 - [-(-1)³/3 + (-1)²/2 + 2.(-1)]
= -8/3 + 2 + 4 - 1/3 - 1/2 + 2
= 8 - 3 - 1/2
= 9/2
NV
Nguyễn Việt Lâm
Giáo viên
29 tháng 1
\(\int\limits^2_{-1}\left(-x^2+x+2\right)dx=\left(-\dfrac{x^3}{3}+\dfrac{x^2}{2}+2x\right)|^2_{-1}=\dfrac{9}{2}\)
AM
10 tháng 2 2022
Ta có: \(\int\dfrac{xdx}{x^2+3}\)
Đặt \(u=x^2+3\left(u>0\right)\)
Có \(du=2xdx\)
\(\Rightarrow\int\dfrac{xdx}{x^2+3}=\)\(\int\dfrac{du}{2u}=\dfrac{1}{2}ln\left(u\right)=\dfrac{1}{2}ln\left(x^2+3\right)\)
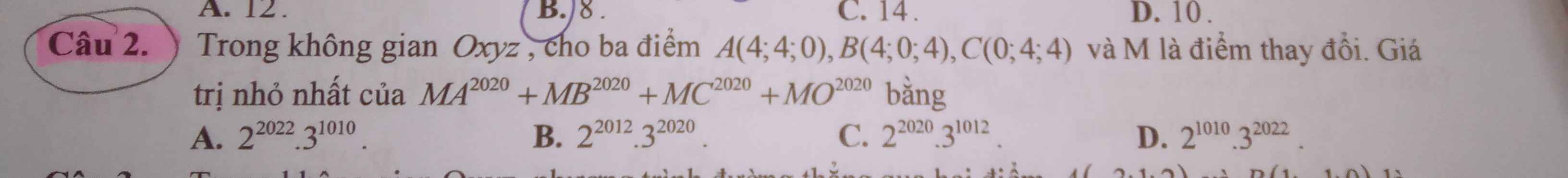
Dễ dàng nhận ra tứ diện OABC là tứ diện đều \(\Rightarrow MA^{2020}+MB^{2020}+MC^{2020}+MO^{2020}\) đạt min khi M trùng trọng tâm tứ diện
Khi đó \(M\left(2;2;2\right)\Rightarrow MA=MB=MC=MO=\sqrt{2^2+2^2+2^2}=2\sqrt{3}\)
\(\Rightarrow P=4.\left(2\sqrt{3}\right)^{2020}=2^{2022}.3^{1010}\)
Thầy ơi thầy giúp em bài này với ạ https://hoc24.vn/cau-hoi/1-limlimits-xrightarrow1dfracx-sqrtx2x-3sqrt3x22-cho-hinh-chop-sabcd-co-day-la-hinh-chu-nhat-ab-a-ad-2a-sa-vuong-goc-voi-day-va-sa-aa-cm-cdperpleftsadright.5799562370088
Em cảm ơn ạ