
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(2^a3^b=\frac{4}{3}\Leftrightarrow2^a.3^{b+1}=4\Leftrightarrow\frac{2^a3^{b+1}}{2^2}=1\Leftrightarrow2^{a-2}3^{b+1}=1.\)
vì 2 và ba nguyên tố cùng nhau nên : \(2^{a-2}.3^{b+1}=1\Leftrightarrow\hept{\begin{cases}a-2=0\\b+1=0\end{cases}\Leftrightarrow\hept{\begin{cases}a=2\\b=-1\end{cases}.}}\)
HOẶC
\(\left(2^{a-2}.3^{b+1}=1\Leftrightarrow2^{a-2}.3^{b+1}=2^0.3^0\Rightarrow\hept{\begin{cases}a-2=0\\b+1=0\end{cases}\Rightarrow}\hept{\begin{cases}a=2\\b=-1\end{cases}}.\right)\)

\(f\left(a,b\right)=a^2+8b^2-6ab+14a-40b+48=3\)
\(\Leftrightarrow f\left(a,b\right)=a^2+8b^2-6ab+14a-40b+45=0\)
\(\Leftrightarrow a^2+2a\left(7-3b\right)+\left(8b^2-40b+45\right)=0\)
Xét \(\Delta'=\left(7-3b\right)^2-\left(8b^2-40b+45\right)=b^2-2b+4=\left(b-1\right)^2+3>0\)
Vậy PT luôn có hai nghiệm phân biệt.
Vì a,b nguyên nên \(b^2-2b+4=k^2\left(k\in N\right)\)
\(\Leftrightarrow k^2-\left(b-1\right)^2=3\Leftrightarrow\left(k-b+1\right)\left(k+b-1\right)=3\)
Xét các trường hợp với k-b+1 và k+b-1 là các số nguyên được :
(b;k) = (0;2) ; (0;-2) ; (2;2) ; (2;-2)
Thay lần lượt các giá trị của b vào f(a,b) = 3 để tìm a.
Vậy : (a;b) = (-9;0) ; (-5;0) ; (-3;2) ; (1;2)

Bài 1:
ĐKXĐ: \(x\ge\dfrac{1}{2}\)
Ta có: \(\sqrt{5x^2}=2x-1\)
\(\Leftrightarrow5x^2=\left(2x-1\right)^2\)
\(\Leftrightarrow5x^2-4x^2+4x-1=0\)
\(\Leftrightarrow x^2+4x-1=0\)
\(\text{Δ}=4^2-4\cdot1\cdot\left(-1\right)=20\)
Vì Δ>0 nên phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{-4-2\sqrt{5}}{2}=-2-\sqrt{5}\left(loại\right)\\x_2=\dfrac{-4+2\sqrt{5}}{2}=-2+\sqrt{5}\left(loại\right)\end{matrix}\right.\)
Bài 1: Bình phương hai vế lên có giải ra được kết quả. Nhưng phải kèm thêm điều kiện $2x-1\geq 0$ do $\sqrt{5x^2}\geq 0$
PT \(\Leftrightarrow \left\{\begin{matrix} 2x-1\geq 0\\ 5x^2=(2x-1)^2\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ x^2+4x-1=0\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ (x+2)^2-5=0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ (x+2-\sqrt{5})(x+2+\sqrt{5})=0\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ x=-2\pm \sqrt{5}\end{matrix}\right.\) (vô lý)
Vậy pt vô nghiệm.


Áp dụng BĐT cauchy, ta có:
\(\sqrt{\left(2y+2z-x\right)\cdot3x}\le\dfrac{2z+2y-x+3x}{2}=\dfrac{2\left(x+y+z\right)}{2}=x+y+z\\ \Leftrightarrow\sqrt{2y+2z-x}\le\dfrac{x+y+z}{\sqrt{3x}}\\ \Leftrightarrow\sqrt{\dfrac{x}{2y+2z-x}}\ge\dfrac{\sqrt{x}}{\dfrac{x+y+z}{\sqrt{3x}}}=\dfrac{x\sqrt{3}}{x+y+z}\)
\(\Leftrightarrow S=\sum\sqrt{\dfrac{x}{2y+2z-x}}\ge\sqrt{3}\left(\dfrac{x}{x+y+z}+\dfrac{y}{x+y+z}+\dfrac{z}{x+y+z}\right)\\ \Leftrightarrow S\ge\sqrt{3}\cdot\dfrac{x+y+z}{x+y+z}=\sqrt{3}\)
Dấu \("="\Leftrightarrow x=y=z\) hay tam giác đều

Câu 2:
a, bạn tự vẽ được nhớ tìm tọa dộ nhé
x 0 0
y 0 0
b, Vì tung độ của điểm nằm trên P có hoành độ bằng 8
=> x = 8
Thay x = 8 vào y = 1/2x^2 ta được :
\(y=\dfrac{1}{2}.64=32\)
Bài 4:
a) Ta có: \(B=\dfrac{x^2+\sqrt{x}}{x-\sqrt{x}+1}+1-\dfrac{2x+\sqrt{x}}{\sqrt{x}}\)
\(=\dfrac{\sqrt{x}\left(x\sqrt{x}+1\right)}{x-\sqrt{x}+1}+1-\dfrac{\sqrt{x}\left(2\sqrt{x}+1\right)}{\sqrt{x}}\)
\(=\sqrt{x}\left(\sqrt{x}+1\right)+1-2\sqrt{x}-1\)
\(=x+\sqrt{x}-2\sqrt{x}\)
\(=x-\sqrt{x}\)

`a)sqrtx=sqrt{16+6sqrt7}`
`=sqrt{9+2.3sqrt7+7}`
`=sqrt{(3+sqrt7)^2}`
`=3+sqrt7`
`b)sqrtx=sqrt{4-2sqrt3}=sqrt{3-2sqrt3+1}=sqrt{(sqrt3-1)^2}=sqrt3-1`
`c)sqrtx=sqrt{13+4sqrt3}=sqrt{12+2.2sqrt3+1}=sqrt{(2sqrt3+1)^2}=2sqrt3+1`
a) \(x=16+6\sqrt{7}\)
\(\Rightarrow\sqrt{x}=\sqrt{16+6\sqrt{7}}\)
\(\Rightarrow\sqrt{x}=\sqrt{7+6\sqrt{7}+9}\)
\(\Rightarrow\sqrt{x}=\sqrt{7+6\sqrt{7}+3^2}\)
\(\Rightarrow\sqrt{x}=\sqrt{\left(\sqrt{7}+3\right)^2}\)
\(\Rightarrow\left(\sqrt{x}\right)^2=\sqrt{\left(\sqrt{7}+3\right)^2}\)
\(\Rightarrow\sqrt{7}+3\)
KL: x=\(\sqrt{7}+3\)

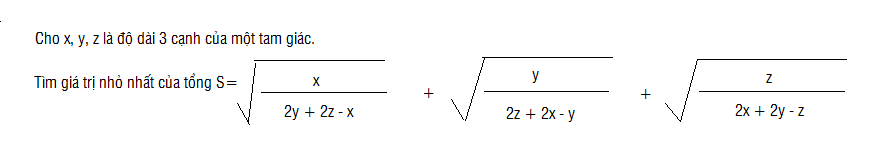
 mọi người giúp mình giải câu 2 3 4 và phần hình học vs ạ. mình cảm ơnnnnnnnnnnnnn
mọi người giúp mình giải câu 2 3 4 và phần hình học vs ạ. mình cảm ơnnnnnnnnnnnnn
Giúp mình với ạ