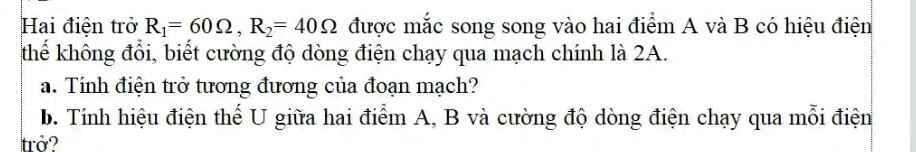Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Điện trở tương đương của đoạn mạch :
\(R_{tđ}=\dfrac{R_1.R_2}{R_1+R_2}=\dfrac{60.40}{60+40}=24\left(\Omega\right)\)
b) Hiệu điện thế giữa hai đầu đoạn mạch :
\(U=I.R_{tđ}=2.24=48\left(V\right)\)
⇒ \(U=U_1=U_2=48\left(V\right)\) (vì R1 // R2)
Cường độ dòng điện chạy qua mỗi điện trở :
\(I_1=\dfrac{U_1}{R_1}=\dfrac{48}{60}=0,8\left(A\right)\)
\(I_2=\dfrac{U_2}{R_2}=\dfrac{48}{40}=1,2\left(A\right)\)
Chúc bạn học tốt

vẽ lại mạch ta có RAM//RMN//RNB
đặt theo thứ tự 3 R là a,b,c
ta có a+b+c=1 (1)
điện trở tương đương \(\dfrac{1}{R_{td}}=\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\) \(\Rightarrow I=\dfrac{U}{R_{td}}=9.\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)\) với a,b,c>0
áp dụng bất đẳng thức cô si cho \(\dfrac{1}{a},\dfrac{1}{b},\dfrac{1}{c}\) \(\Rightarrow\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\ge\dfrac{3}{\sqrt[3]{abc}}\ge\dfrac{3}{\left(\dfrac{a+b+c}{3}\right)}=\dfrac{9}{a+b+c}=9\)
\(\Leftrightarrow9\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)\ge81\Leftrightarrow I\ge81\) I min =81 ( úi dồi ôi O_o hơi to mà vẫn đúng đá nhỉ)
dấu ''='' xảy ra \(\Leftrightarrow a=b=c\left(2\right)\)
từ (1) (2) \(\Rightarrow a=b=c=\dfrac{1}{3}\left(\Omega\right)\)
vậy ... (V LUN MẤT CẢ BUỔI TỐI R BÀI KHÓ QUÁ EM ĐANG ÔN HSG À )

a. \(R=R1+R2+R3=5+6+15=26\Omega\)
b. \(I=I1=I2=I3=1A\left(R1ntR2ntR3\right)\)
\(\left\{{}\begin{matrix}U=IR=1.26=26\left(V\right)\\U1=I1.R1=1.5=5\left(V\right)\\U2=I2.R2=1.6=6\left(V\right)\\U3=I3.R3=1.15=15\left(V\right)\end{matrix}\right.\)
c. \(R'=U:I'=26:0,5=52\Omega\)
\(\Rightarrow R_x=R'-\left(R1+R2\right)=52-\left(5+6\right)=41\Omega\)


mình giải rồi nhé, bạn có thể lướt xuống để nhận lời giải

a,\(\Rightarrow\)R4 nt R5 nt {(R1 nt R3)//R2)}(goi R3=x(\(\Omega\))
\(\Rightarrow Rtd=R4+R5+\dfrac{R2\left(R1+x\right)}{R2+R1+x}=\dfrac{U}{Ia1}=\dfrac{6}{0,5}=12\Omega\)
\(\Rightarrow3+6+\dfrac{4\left(6+x\right)}{4+6+x}=12\Rightarrow x=R3=6\Omega\)
b, \(\Rightarrow\)R5 nt {R3 // {R2 nt (R1//R4)}} lay R3=6(om)
\(\Rightarrow Ia1=\dfrac{U}{Rtd}=\dfrac{6}{R5+\dfrac{R3\left\{R2+\dfrac{R1R4}{R1+R4}\right\}}{R3+R2+\dfrac{R1R4}{R1+R4}}}=\dfrac{6}{9}=\dfrac{2}{3}A\)
\(\Rightarrow Ia1=Ia2+I1\Rightarrow Ia2=Ia1-I1=\dfrac{2}{3}-I1\)
\(\Rightarrow U124=U-U5=6-Ia1.R5=2V\Rightarrow I14=\dfrac{U124}{R124}=\dfrac{2}{R2+\dfrac{R1R4}{R1+R4}}=\dfrac{1}{3}A\Rightarrow U14=U1=I14.R14=\dfrac{2}{3}V\Rightarrow I1=\dfrac{U1}{R1}=\dfrac{1}{9}A\Rightarrow Ia2=\dfrac{2}{3}-\dfrac{1}{9}=\dfrac{5}{9}A\)


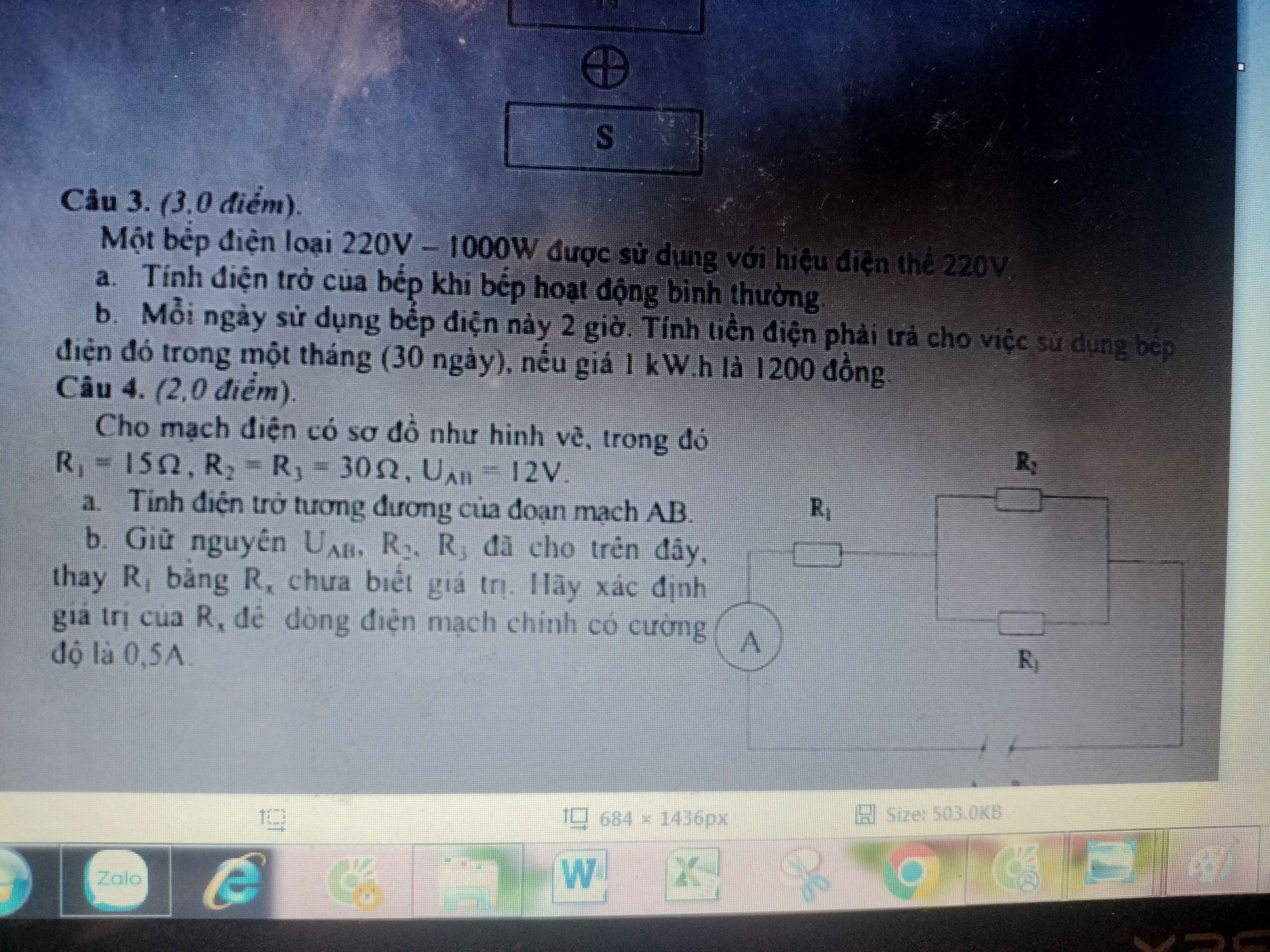
Câu 4:
a. Điện trở tương đương của đoạn mạch AB là: \(R_{AB}=R_1+\dfrac{R_2R_3}{R_2+R_3}=30\left(\Omega\right)\)
b. Điện trở tương đương của đoạn mạch AB là:
\(R_{AB}'=R_x+\dfrac{R_2R_3}{R_2+R_3}=R_x+15\)
Cường độ dòng điện qua mạch chính là:
\(I=\dfrac{U_{AB}}{R_{AB}'}=\dfrac{12}{R_x+15}=0,5\left(A\right)\)
\(\Rightarrow R_x=9\left(\Omega\right)\)
Câu 3:
a. Điện trở của bếp khi bếp hoạt động bình thường:
\(R=\dfrac{U_{đm}^2}{P_{đm}}=48,4\left(\Omega\right)\)
b. Điện năng tiêu thụ của bếp điện trong một tháng là:
\(A=UIt=Pt=1000.2.30=60000\left(Wh\right)=60\left(kWh\right)\)
Số tiền cần phải trả là: \(60.1200=72000\left(đồng\right)\)